前面的分析都是基于“线性假设“，它的优点是实际中简单有效，而且理论上有VC 维的保证；然而，面对线性不可分的数据时（实际中也有许多这样的例子），线性方法不那么有效。
1，二次假设
对于下面的例子，线性假设显然不奏效：
我们可以看出，二次曲线（比如圆）可以解决这个问题。 接下来就分析如何通过二次曲线假设解决线性方法无法处理的问题，进而推广到多次假设。
对于上面的例子，我们可以假设分类器是一个圆心在原点的正圆，圆内的点被分为+1，圆外的被分为-1，于是有：
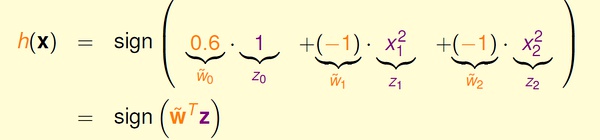在上面的式子中，将(0.6, -1, -1) 看做向量w，将(1, x1^2, x2^2) 看做向量z，这个形式和传统的线性假设很像。可以这样理解，原来的x 变量都映射到了z-空间，这样，在x-空间中线性不可分的数据，在z-空间中变得线性可分；然后，我们在新的z-空间中进行线性假设。
在数学上，通过参数w 的取值不同，上面的假设可以得到正圆、椭圆、双曲线、常数分类器，它们的中心都必须在原点。如果想要得到跟一般的二次曲线，如圆心不在原点的圆、斜的椭圆、抛物线等，则需要更一般的二次假设。
2，非线性转换
进行非线性转换的学习步骤
这里的非线性转换其实也是特征转换(feature transform)，在特征工程里很常见。
3，非线性转换的代价
所谓”有得必有失“，将特征转换到高次空间，我们需要付出学习代价（更高的模型复杂度）。
x-空间的数据转换到z-空间之后，新的假设中的参数数量也比传统线性假设多了许多：
根据之前分析过的，vc 维约等于自由变量（参数）的数量，所以新假设的dvc 急速变大，也就是模型复杂大大大增加。
回顾机器学习前几讲的内容，我们可以有效学习的条件是：（1）Ein(g) 约等于 Eout(g)；（2）Ein(g) 足够小。
当模型很简单时（dvc 很小），我们更容易满足（1）而不容易满足（2）；反之，模型很复杂时（dvc很大），更容易满足（2）而不容易满足（1）。
看来选择合适复杂度的model 非常trick :-)
4，假设集
前面我们分析的非线性转换都是多项式转换(polynomial transform)。
我们将二次假设记为H2，k次假设记为Hk。显然，高次假设的模型复杂度更高。
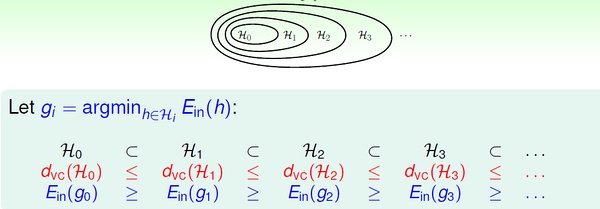
也就是说，高次假设对数据拟合得更充分，Ein 更小；然而，由于付出的模型复杂度代价逐渐增加，Eout 并不是一直随着Ein 减小。
上图我们在前面也见过。实际工作中，通常采用的方法是：先通过最简单的模型（线性模型）去学习数据，如果Ein 很小了，那么我们就认为得到了很有效的模型；否则，转而进行更高次的假设，一旦获得满意的Ein 就停止学习（不再进行更高次的学习）。 总结为一句话：linear/simpler model first !