1， 线性回归问题
例如，信用卡额度预测问题：特征是用户的信息（年龄，性别，年薪，当前债务，…），我们要预测可以给该客户多大的信用额度。 这样的问题就是回归问题。 目标值y 是实数空间R。
线性回归假设
线性回归假设的思想是：寻找这样的直线/平面/超平面，使得输入数据的残差最小。
通常采用的error measure 是squared error:
2，线性回归算法
squared error 的矩阵表示：
Ein 是连续可微的凸函数，可以通过偏微分求极值的方法来求参数向量w。
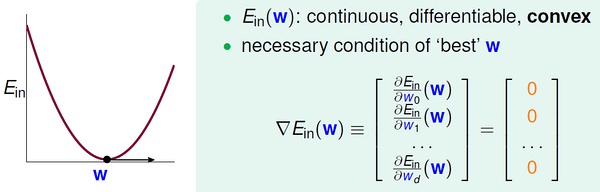求得Ein(w) 的偏微分：
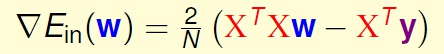另上式等于0，即可以得到向量w
上面分两种情况来求解w。当XTX(X 的转置乘以X) 可逆时，可以通过矩阵运算直接求得w；不可逆时，直观来看情况就没这么简单。
实际上，无论哪种情况，我们都可以很容易得到结果。因为许多现成的机器学习/数学库帮我们处理好了这个问题，只要我们直接调用相应的计算函数即可。有些库中把这种广义求逆矩阵运算成为 pseudo-inverse。
到此，我们可以总结线性回归算法的步骤（非常简单清晰）：
3，线性回归是一个“学习算法” 吗？
乍一看，线性回归“不算是”机器学习算法，更像是分析型方法，而且我们有确定的公式来求解w。
实际上，线性回归属于机器学习算法：
（1） 对Ein 进行优化。
（2）得到Eout 约等于 Ein。
（3）本质上还是迭代提高的：pseudo-inverse 内部实际是迭代进行的。
经过简单的分析证明可以得到Ein,Eout 的平均范围（过程见林轩田视频），画出学习曲线
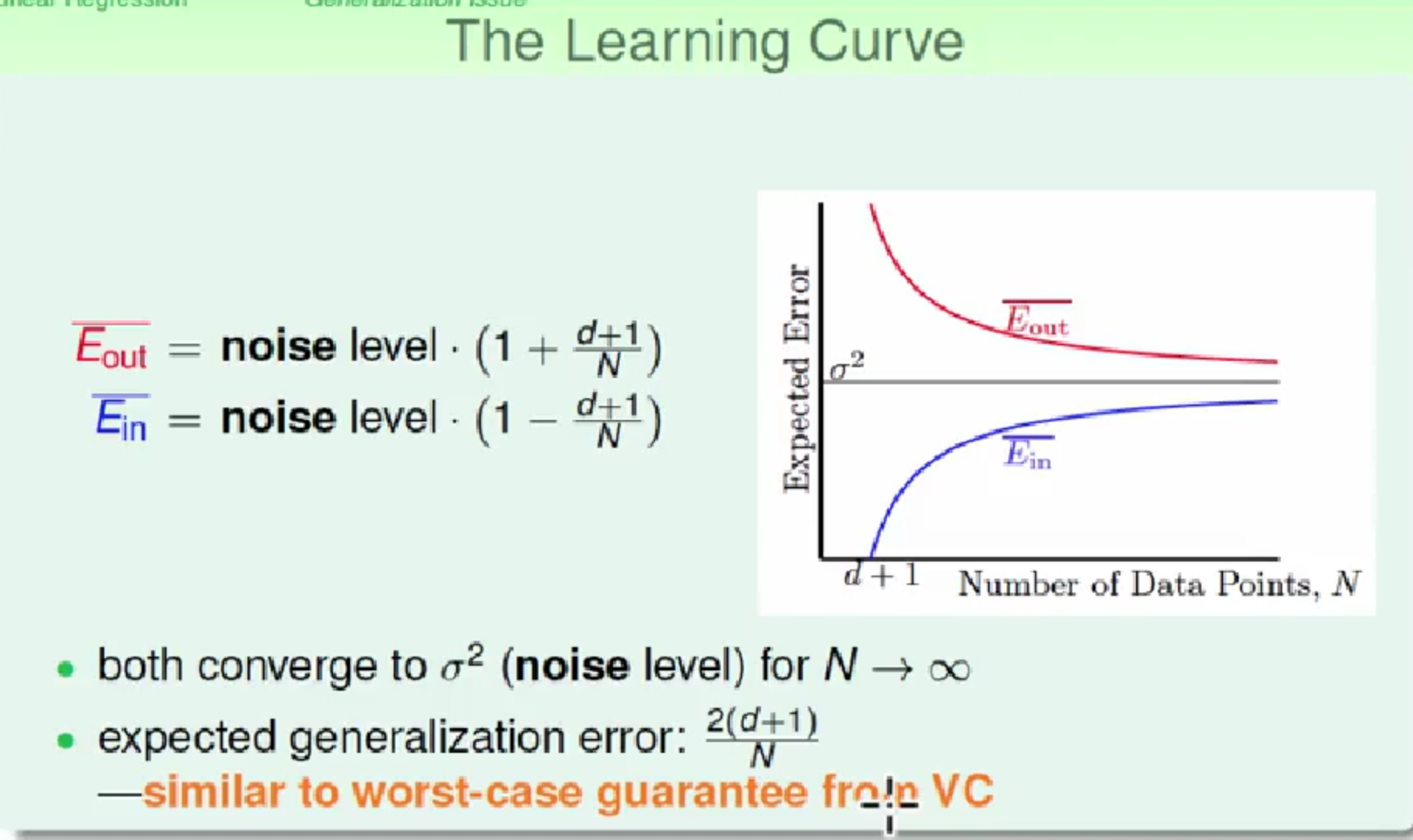4， 线性回归与线性分类器
比较一下线性分类与线性回归：
之所以能够通过线程回归的方法来进行二值分类，是由于回归的squared error 是分类的0/1 error 的上界，我们通过优化squared error，一定程度上也能得到不错的分类结果；或者，更好的选择是，将回归方法得到的w 作为二值分类模型的初始w 值。
