上一讲的最后得到了VC bound，这一讲对VC维理论进行理解，这是机器学习（最）重要的理论基础。
我们先对前面得到的生长函数和VC bound 做一点小的修改。
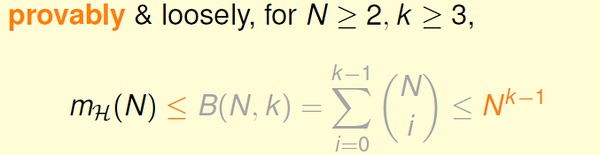
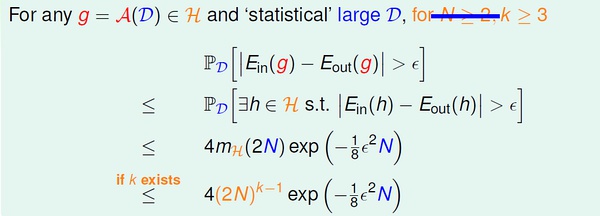
1，VC 维的定义
VC Demension: 对于假设空间H，满足生长函数m(N) = 2^N 的最大的N， 记为dvc(H).
可知，dvc(H) 比H 的最小突破点k 小1，即 dvc(H) = k-1.
2维感知机的VC维是3.
2，感知机的VC维
我们已经知道，2维感知机的VC维是3.
对于d 维感知机，我们猜测它的VC 维是 d+1 ?
对此，我们只要证明 dvc >= d+1 && dvc <= d+1.
(1) 证明 dvc >= d+1
对于d 维空间的任意输入数据x1, 都增加一个分量x10, 取值恒为1.
即 x1 = (1, x11, x12, … , x1d)。 （x1 是一个向量）
取组特殊的输入数据
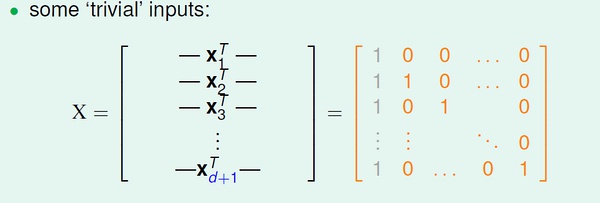对于上面的d+1 个输入数据，我们可以求得向量w :
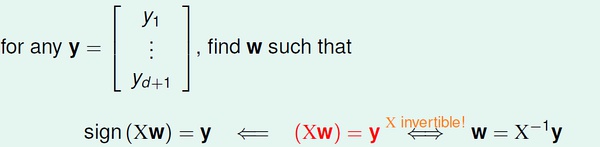
也就是说，这样的d+1 个输入数据可以被d 维感知机打散(shattered), 所以有 dvc >= d+1.
(2) 证明 dvc <= d+1
对于d 维空间的输入数据：
也就是说，不可能存在d+2 个线性独立的输入数据。其中，线性组合中的系数可能为正、负或零，但是不全为零。
等式两边都乘以 w 向量：
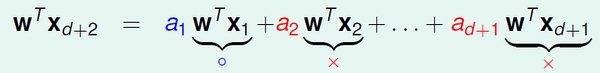
假设这d+2 个数据都可以被打散。那么我们可以对 wx 随意取值（-1 或 +1），上式都应该能够满足。然而，对于这样的情况：当系数a 为正数时，wx 取+1，反之w*x 取-1，式子右边一定大于0；此时式子左边就无法取-1，与假设矛盾。
所以d 维感知机无法打散 d+2 个点，也就是说VC 维最大只能是 d+1.
综合（1）（2），证得 dvc = d+1.
3，VC 维的物理意义
VC维可以反映假设H 的强大程度(powerfulness)，VC 维越大，H也越强，因为它可以打散更多的点。
通过对常见几种假设的VC 维的分析，我们可以得到规律：VC 维与假设参数w 的自由变量数目大约相等。
例如，对于2维感知机，w = (w0, w1, w2)，有三个自由变量，dvc = 3
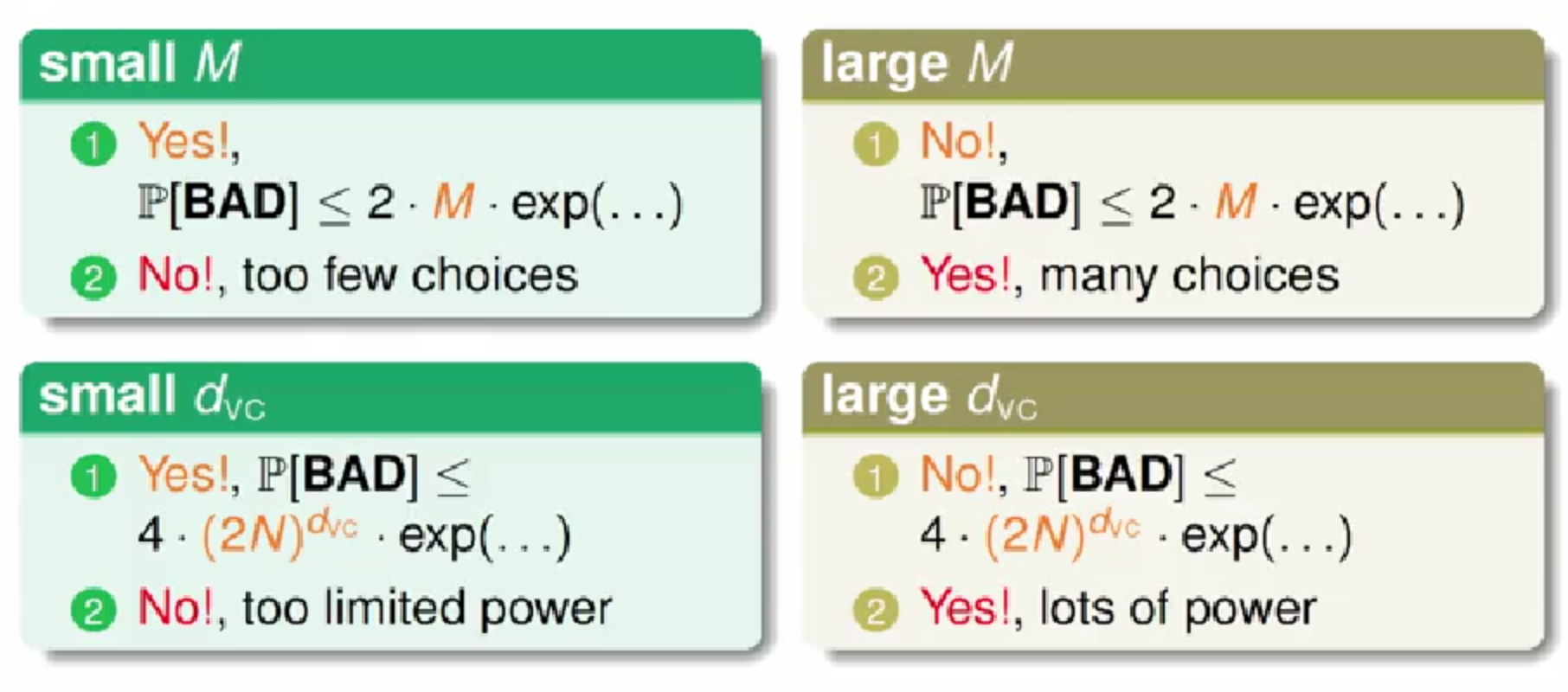
4，VC 维的解释
VC 维反映了假设H 的强大程度，然而VC 维并不是越大越好。
通过一些列数学推导，我们得到：
上面的”模型复杂度“ 的惩罚(penalty)，基本表达了模型越复杂（VC维大），Eout 可能距离Ein 越远。
下面的曲线可以更直观地表示这一点：
模型较复杂时(dvc 较大)，需要更多的训练数据。 理论上，数据规模N 约等于 10000dvc（称为采样复杂性，sample complexity）；然而，实际经验是，只需要 N = 10dvc.
造成理论值与实际值之差如此之大的最大原因是，VC Bound 过于宽松了，我们得到的是一个比实际大得多的上界。
即便如此，VC Dimension & VC bound 依然是分析机器学习模型的最重要的理论工具。