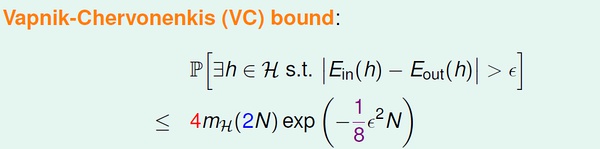界函数（bounding function）的概念
是指当（最小）突破点为k 时，生长函数m(N) 可能的最大值，记为B(N, k)。
显然，当k=1时，B(N, 1) = 1; 当k > N 时，B(N,k) = 2^N; 当k = N 时，B(N,k)=2^N - 1.
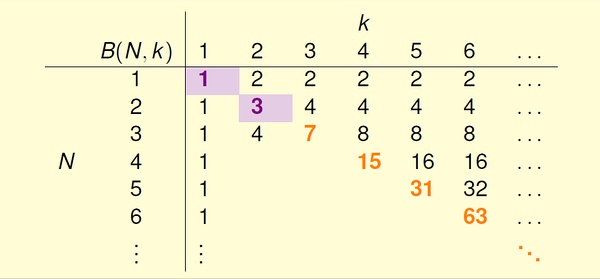
于是很容易得到Bounding function table:
证明：
我们考虑B(4, 3)，对应的数据量是4 (x1, x2, x3, x4)，从这四个数据的角度看应该有B(4,3)个有效的dichotomies。
如果我们遮住其中一个 数据（比如x4），余下的dichotomies去重后，不超过B(3,3) 个。（否则就违背了突破点在3）。显然， B(4,3) <= 2 * B(3,3)。
也就是说，当扩展为(x1,x2,x3,x4)时，(x1,x2,x3)上的dichotomies 只有部分被重复复制了（最多一次）。
于是可以设 被复制的dichotomies 数量为a，未被复制的数量为b。（0 <= a,b <= B(3,3) )
可以知道，B(3,3) = a+b; B(4,3) = 2*a + b.
我们假设a > B(3,2)，这样，当扩展到(x1,x2,x3,x4) 时，有大于B(3,2) 的(x1,x2,x3) 上的dichotomies 被复制。此时在(x1,x2,x3) 中一定能够找到两个点被打散(shatter)而且被复制了，由于被复制，对月这些dichotomies，x4可以取两个不同类别的值，因此在(x1,x2,x3,x4) 中一定能找到3个点被打散了。这与”3”是突破点相违背。假设不成立，所以a <= B(3,2)。
所以，我们得到：B(4,3) = 2*a + b <= B(3,3) + B(3,2).
对于任意N > k, 利用上述思路，可以证明 B(N,k) <= B(N-1, k) + B(N-1,k-1).
有了递推不等式，通过数学归纳法，我们证明下面的Bounding Function (N > k) :
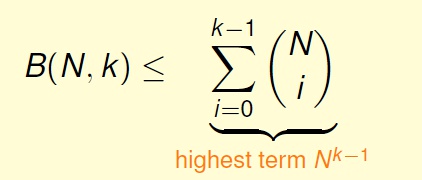这个式子显然是多项式的，最高次幂是 k-1。
所以我们得到结论：如果突破点存在（有限的正整数），生长函数m(N) 是多项式的。
既然得到了m(N) 的多项式上界，我们希望对之前的不等式（如下图）中M 进行替换。
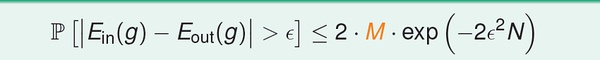然而直接替换是存在问题的。主要问题就是Eout(h)，out 的空间是无穷大的，通过将Eout 替换为验证集(verification set) 的Ein’ 来解决这个问题。最后我们得到下面的VC bound:
