回顾:学习的可行性?
最重要的是公式:
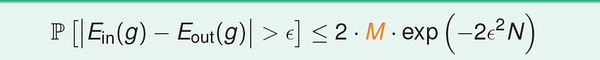
(1) 假设空间H有限(M),且训练数据足够大,则可以保证测试错误率Eout 约等于训练错误率Ein;
(2)如果能得到Ein 接近于零,根据(1),Eout 趋向于零。
以上两条保证的学习的可能性。
可知,假设空间H 的大小M 至关重要,我们接下来会力求找一个H 大小的上界。
M存在重要的trade-off 思想:
(1)当M 很小,那么坏数据出现的概率非常小(见第四讲分析),学习是有效的;但是由于假设空间过小,我们不一定能找到一个方案,可以使训练误差接近零;
(2)反之,若M 很大,坏数据出现的概率会变大。
若假设空间无限大(比如感知机),学习一定是无效的吗?这门在下面力图回答这个问题。
假设空间H 大小:M
根据上面的公式,当M 无限大时是无法有效学习的;主要是我们在计算M 是通过UNION BOUND 的方式,这样得到的上界太宽松了;实际上,由于不同假设下发生坏事情是有很多重叠的,其实我们可以得到比M小得多的上界。
我们希望将这么多的假设进行分组,根据组数来考虑假设空间大小。
后面的讨论都是针对批量的二值分类问题。
这个思想的关键是,我们从有限个输入数据的角度来看待假设的种类。
(1)最简单的情形,只有一个输入数据时,我们最多只有两种假设:h1(x) = +1 or h2(x) = -1 。
(2)输入数据增加到两个,最多可以有四种假设:
h1(x1)=1, h1(x2)=1;
h2(x1)=-1, h2(x2)=1;
h3(x1)=1, h3(x2)=-1;
h4(x1)=-1, h4(x2)=-1.
依次类推, 对于k 个输入数据,最多有2^k 种假设。
上面阐述的是理想、极端情况,实际上,在实际学习中我们得不到如此之多的假设。例如,对于2维感知机(输入为平面上的点),输入数据为3个时,下面这种假设是不存在的:
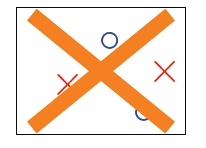
(圆圈和叉代表两种不同分类,这种情形也就是线性不可分)。
我们尝试猜测,当k 很大时,有效假设的数量远小于 2^k ?
定义”dichotomy”: hypothesis ‘limited’ to the eyes if x1, x2, …, xn
也就是相当于我们前面描述的,从输入数据的角度看,有效假设的种类。
输入规模为N时,dichotomies 的一个宽的上界是 2^N.
定义关于数据规模N 的生长函数(growth function):数据规模为N 时,可能的dichotomy 的数量,记为m(N)。
下面列举几种生长函数:
(1)X=R(一维实数空间),h(x) = sign(x-a), a 是参数。
它的生长函数: m(N) = N + 1 ; 当N > 1时,m(N) < 2^N
(2)X=R, h(x) = 1 iff x>=a or x<b, -1 otherwise. 有两个参数 a, b.
它的生长函数:m(N) = 0.5N^2 + 0.5N + 1; 当 N>2 时, m(N) < 2^N
(3)X=R^2(二维实数空间),h是一个任意凸多边形,多边形内部的为1,外部的为-1。
它的生长函数:m(N) = 2^N

我们引入一个重要概念:突破点(break point):
对于某种假设空间H,如果m(k)<2^k, 则k 是它的突破点。
对于上面提到的三个例子,(1)的突破点是2,3,4… (2)的图破点是3,4,… (3)没有突破点。
注意:如果k 是突破点,那么k+1, k+2, … 都是突破点。
对于感知机,我们不知道它的生长函数,但是我们知道它的第一个突破点是4, m(4)=14 < 16
对于后面的证明,突破点是一个很重要的概念。