机器学习的可行性分析。
一， 第一条准则： 没有免费的午餐！(no free lunch !)
给一堆数据D， 如果任何未知的f （即建立在数据D上的规则）都是有可能的，那么从这里做出有意义的推理是不可能的！！ doomed !!
如下面这个问题无解（或者勉强说没有唯一解）
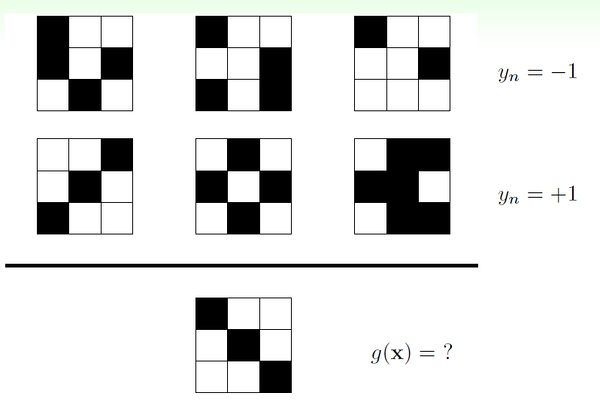
下面这题也是如此：
如何解决上述存在的问题？ 答：做出合理的假设。
关于罐子里选小球的推论
霍夫丁不等式(Hoeffding’s Inequality)
这里v 是样本概率；u 是总体概率
罐子理论与学习问题的联系
对于一个固定的假设h， 我们需要验证它的错误率；然后根据验证的结果选择最好的h。
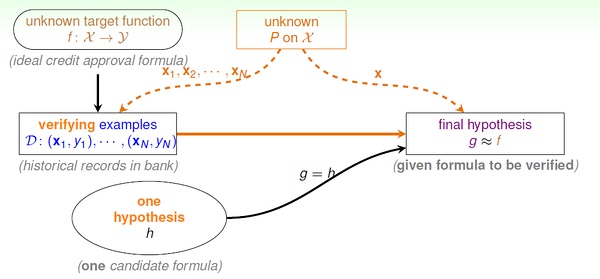
Real Learning
面对多个h 做选择时，容易出现问题。比如，某个不好的h 刚好最初的”准确“ 的假象。
随着h 的增加，出现这种假象的概率会增加。
发生这种现象的原因是训练数据质量太差。
对于某个假设h， 当训练数据对于h 是BAD sample 时， 就可能出现问题。
因此，我们希望对于我们面对的假设空间，训练数据对于其中的任何假设h 都不是BAD sample。
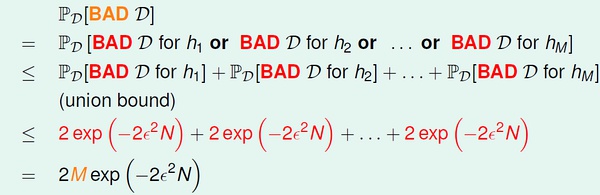
所以，当假设空间有限时（大小为M）时， 当N 足够大，发生BAD sample 的概率非常小。 此时学习是有效的。
当假设空间无穷大时（例如感知机空间），我们下一次继续讨论。（提示：不同假设遇到BAD sample 的情况会有重叠）