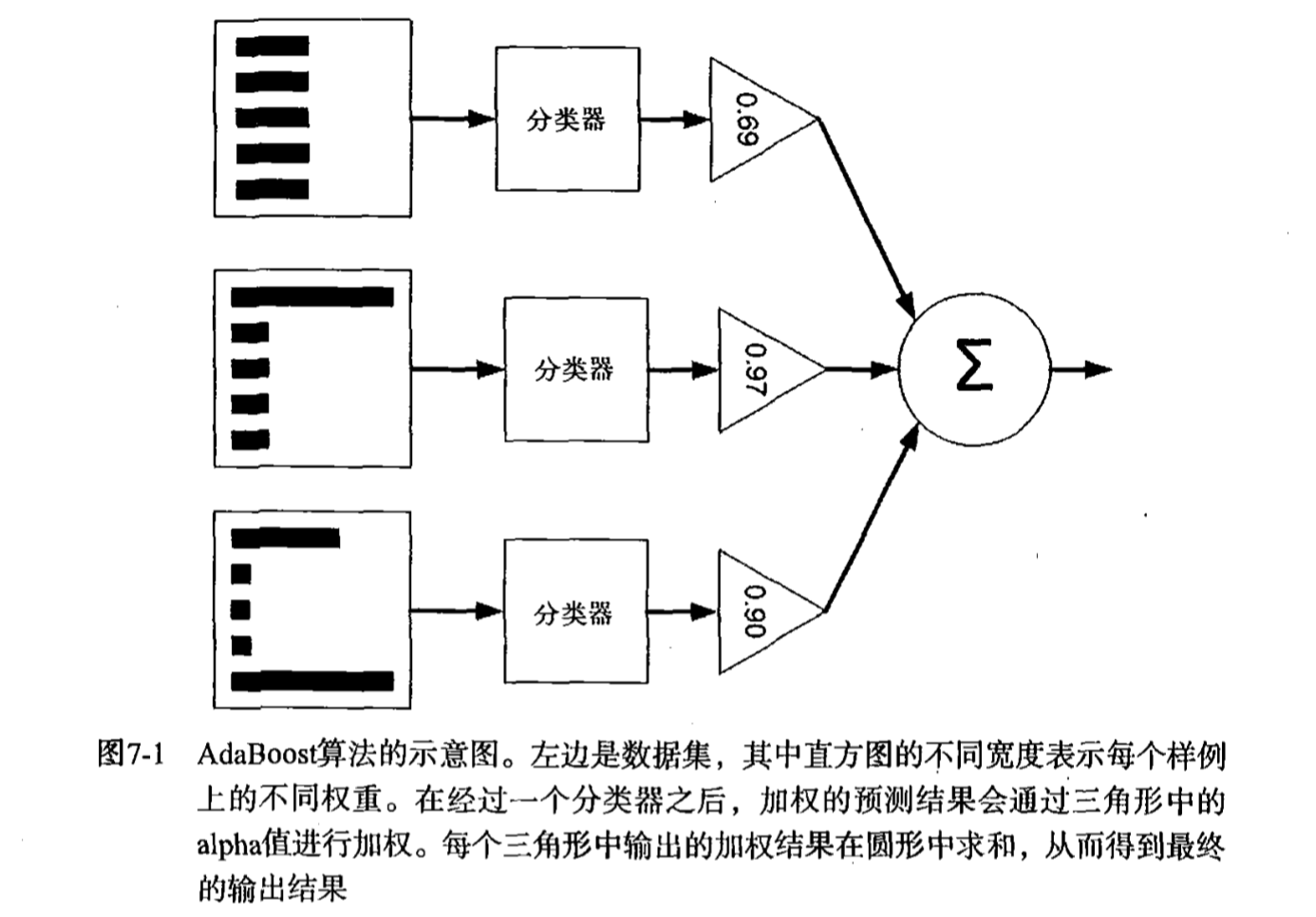
在介绍AdaBoost算法之前,需要了解一个类似的算法,装袋算法(bagging),bagging是一种提高分类准确率的算法,通过给定组合投票的方式,获得最优解。比如你生病了,去n个医院看了n个医生,每个医生给你开了药方,最后的结果中,哪个药方的出现的次数多,那就说明这个药方就越有可能性是最优解,这个很好理解。而bagging算法就是这个思想。
而AdaBoost算法的核心思想还是基于bagging算法,但是他又一点点的改进,上面的每个医生的投票结果都是一样的,说明地位平等,如果在这里加上一个权重,大城市的医生权重高点,小县城的医生权重低,这样通过最终计算权重和的方式,会更加的合理,这就是AdaBoost算法。AdaBoost算法是一种迭代算法,只有最终分类误差率小于阈值算法才能停止,针对同一训练集数据训练不同的分类器,我们称弱分类器,最后按照权重和的形式组合起来,构成一个组合分类器,就是一个强分类器了。算法的只要过程:
1、对D训练集数据训练处一个分类器Ci
2、通过分类器Ci对数据进行分类,计算此时误差率
3、把上步骤中的分错的数据的权重提高,分对的权重降低,以此凸显了分错的数据。
算法流程如下:


基于单层决策树构建弱分类器
单层决策树是一种简单的决策树。前面我们已经介绍了决 策树的工作原理,接下来将构建一个单层决策树,而它仅基于单个特征来做决策。由于这棵树只 有一次分裂过程,因此它实际上就是一个树桩。
单层决策树生成函数
伪代码如下

def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):#just classify the data
retArray = ones((shape(dataMatrix)[0],1))
if threshIneq == 'lt':
retArray[dataMatrix[:,dimen] <= threshVal] = -1.0
else:
retArray[dataMatrix[:,dimen] > threshVal] = -1.0
return retArray
def buildStump(dataArr,classLabels,D):
dataMatrix = mat(dataArr); labelMat = mat(classLabels).T
m,n = shape(dataMatrix)
numSteps = 10.0; bestStump = {}; bestClasEst = mat(zeros((m,1)))
minError = inf #init error sum, to +infinity
for i in range(n):#loop over all dimensions
rangeMin = dataMatrix[:,i].min(); rangeMax = dataMatrix[:,i].max();
stepSize = (rangeMax-rangeMin)/numSteps
for j in range(-1,int(numSteps)+1):#loop over all range in current dimension
for inequal in ['lt', 'gt']: #go over less than and greater than
threshVal = (rangeMin + float(j) * stepSize)
predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal)#call stump classify with i, j, lessThan
errArr = mat(ones((m,1)))
errArr[predictedVals == labelMat] = 0
weightedError = D.T*errArr #calc total error multiplied by D
#print "split: dim %d, thresh %.2f, thresh ineqal: %s, the weighted error is %.3f" % (i, threshVal, inequal, weightedError)
if weightedError < minError:
minError = weightedError
bestClasEst = predictedVals.copy()
bestStump['dim'] = i
bestStump['thresh'] = threshVal
bestStump['ineq'] = inequal
return bestStump,minError,bestClasEst
完整adaboost算法的实现

def adaBoostTrainDS(dataArr,classLabels,numIt=40):
weakClassArr = []
m = shape(dataArr)[0]
D = mat(ones((m,1))/m) #init D to all equal
aggClassEst = mat(zeros((m,1)))
for i in range(numIt):
bestStump,error,classEst = buildStump(dataArr,classLabels,D)#build Stump
#print "D:",D.T
alpha = float(0.5*log((1.0-error)/max(error,1e-16)))#calc alpha, throw in max(error,eps) to account for error=0
bestStump['alpha'] = alpha
weakClassArr.append(bestStump) #store Stump Params in Array
#print "classEst: ",classEst.T
expon = multiply(-1*alpha*mat(classLabels).T,classEst) #exponent for D calc, getting messy
D = multiply(D,exp(expon)) #Calc New D for next iteration
D = D/D.sum()
#calc training error of all classifiers, if this is 0 quit for loop early (use break)
aggClassEst += alpha*classEst
#print "aggClassEst: ",aggClassEst.T
aggErrors = multiply(sign(aggClassEst) != mat(classLabels).T,ones((m,1)))
errorRate = aggErrors.sum()/m
print "total error: ",errorRate
if errorRate == 0.0: break
return weakClassArr,aggClassEst
向量D非常重要,包含每个数据点的权重,一开始这些权重都被赋予相同的值,接着增加错分数据的权重,降低正确分类数据的权重,d是一个概率分布向量, 因此所有元素之和为1,为满足要求,需要初始化。同时用aggClassEst,记录每个数据点的类别估计累计值。
测试算法
一旦拥有了多个弱分类器以及其对应的alpha值,进行测试就变得相对容易了,我们所要做的就是将弱分类器的训练过程从程序中抽出来,然后应用到某个具体实例上去。
def adaClassify(datToClass,classifierArr):
dataMatrix = mat(datToClass)#do stuff similar to last aggClassEst in adaBoostTrainDS
m = shape(dataMatrix)[0]
aggClassEst = mat(zeros((m,1)))
for i in range(len(classifierArr)):
classEst = stumpClassify(dataMatrix,classifierArr[i]['dim'],\
classifierArr[i]['thresh'],\
classifierArr[i]['ineq'])#call stump classify
aggClassEst += classifierArr[i]['alpha']*classEst
print aggClassEst
return sign(aggClassEst)


非均衡分类问题
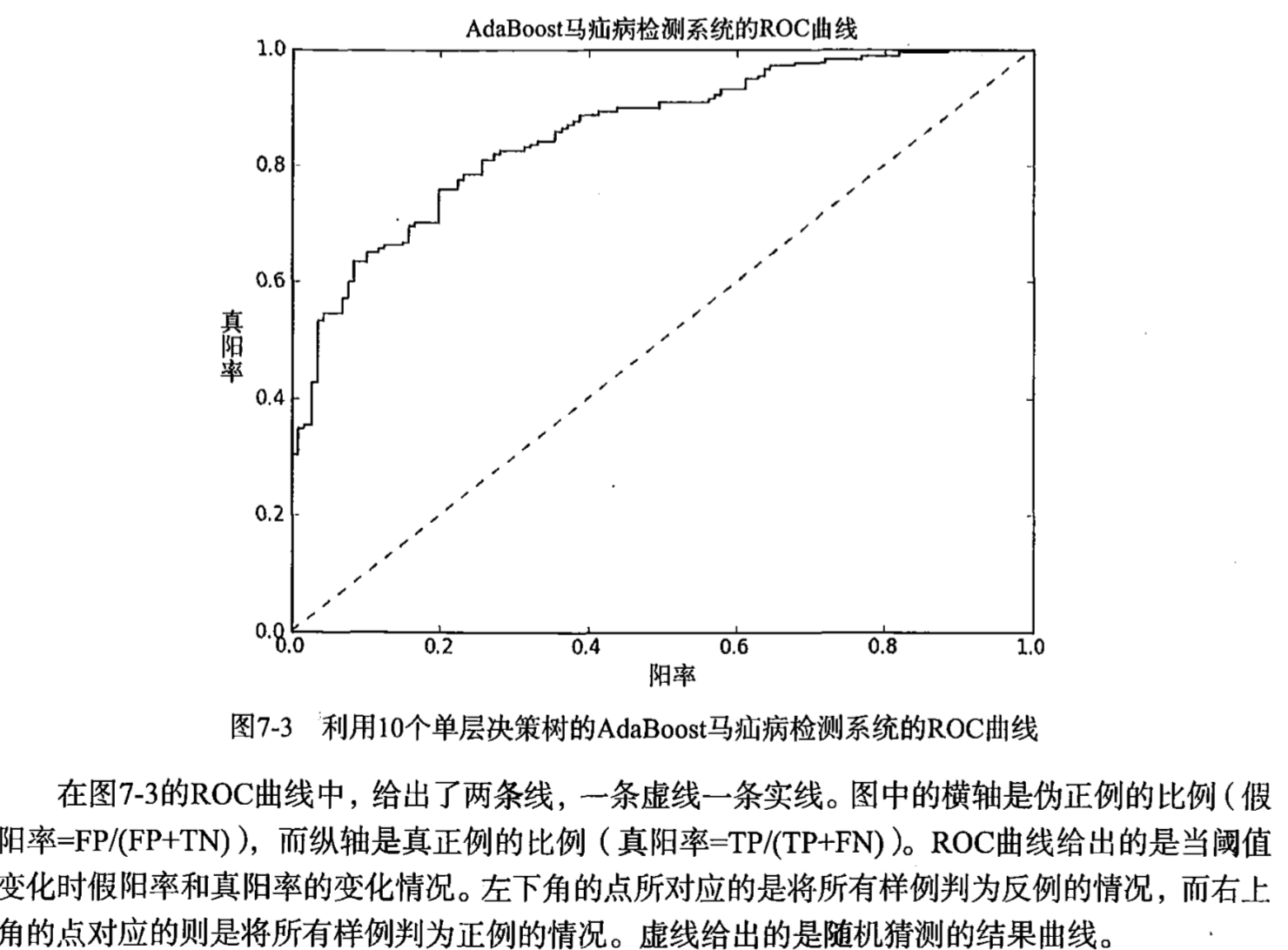
其他分类性能指标:正确率,召回率及roc曲线
 我们可以用roc曲线解决这个问题
我们可以用roc曲线解决这个问题