图像识别初步 - 良有以也

本文主要包括以下内容

模式与模式识别的基本概念
过度拟合
最小距离分类器
基于相关的模板匹配
本章的典型案例分析
- 基于最小距离分类器的鸾尾属植物分类
- 基于相关技术的图像模式匹配

模式识别概述

模式识别(Pattern Recognition)是人类的一项基本智能，在日常生活中，人们经常在进行“模式识别”。随着20世纪40年代计算机的出现以及50年代人工智能的兴起，人们当然也希望能用计算机来代替或扩展人类的部分脑力劳动。（计算机）模式识别在20世纪60年代初迅速发展并成为一门新学科。

模式与模式识别

模式是由确定的和随机的成分组成的物体、过程和事件。在一个模式识别问题中，它是我们识别的对象。
模式识别是指对表征事物或现象的各种形式的（数值的、文字的和逻辑关系的）信息进行处理和分析，以对事物或现象进行描述、辨认、分类和解释的过程，简单的说就是应用计算机对一组事件或过程进行鉴别和分类。
我们所指的模式识别主要是对语音波形、地痕波、心电图、脑电图、图片、照片、文字、符号、生物的传感器等对象进行测量的具体模式进行分类和辨识。

图像识别
将模式识别的方法和技术应用千图像领域，即当识别的对象是图像时就称为图像识别口虽然对我们人类而言，理解和识别所看见的东西似乎是一件再平常不过的事情，让计算机具有类似的智能却是一项极具挑战性的任务，然而两者在很多环节上是相似的，下面让我们从熟悉的人类视觉过程开始，认识机器的图像识别机理。
图形刺激作用于感觉器官，人们辨认出它是经验过的某一图形的过程，也叫图像再认。所以说在图像识别中，既要有当时进入感官的信息，也要有记忆中存储的信息。只有通过存储的信息与当前的信息进行比较的加工过程，才能实现对图像的再认。这一点和计算机的识别过程中相似，即需要先学习一些已经类别的样本（训练样本），才能识别那些类别未知的新样本（测试样本）。
图像识别可能是以图像的主要特征为基础的。每个图像都有它的特征，如字母A有个尖、P有个圈、而Y的中心有个锐角等。相关研究表明，识别时视线总是集中在图像的主要特征上，也就是集中在图像轮廓曲度最大或轮廓方向突然改变的地方，这些地方的信息量最大.并且眼睛的扫描路线也总是依次从一个特征转到另一个特征上。由此可见，在图像识别过程中，知觉机制必须排除输入的多余信息，抽出关键的信息。同时，在大脑里必定有一个负责整合信息的机制，它能把分阶段获得的信息整理成一个完整的知觉映象。这一点正好说明了图像识别中特征提取的必要性。
图像识别中著名的模板匹配模型认为，要识别某个图像，必须在过去的经验中有这个图像的记忆模式，又叫模板。当前的刺激如果能与大脑中的模板相匹配，这个图像就被识别了。例如有一个字母人如果在脑中有个A模板，字母A的大小、方位、形状都与这个A模板完全一致，字母A就被识别了。但这种模型强调图像必须与脑中的模板完全匹配才能成功识别，而事实上人不仅能识别与脑中的模板完全一致的团像，也能识别与模板不完全一致的图像。例如，人们不仅能识别某一个具体的字母A,也能识别印刷体的、手写体的、方向不正大小不同的各种字母A。这就提示我们匹配过程不是基于完全相同的比较而是基于某种相似性的度至。

关键概念

下面介绍一些识别中常用的重要概念。

模式类(pattern class): 指共享一组共同属性（或特征）的模式集合，通常具有相同的来源。
特征(feature): 指一种模式区别于另一种模式的相应（本质）特点或特性，是通过测量和或处理能够抽取的数据
噪声(noise): 指与模式处理（特征抽取中的误差）和（或）训练样本联合的失真．它对系统的分类能力（如识别）产生影响．
分类／识别(classfication/Recognition): 指根据特征将模式分配给不同的模式类，识别出模式的类别的过程．
分类器(classifier): 指为了实现分类而建立起来某种计算模型，它以模式特征为输入，输出该模式所属的类别信息．
训练样本(training sample): 指一些类别信息已知的样本，通常使用它们来训练分类器．
训练集合(training set) : 训练样本所组成的集合．
训练学习(training learning): 指根据训练样本集合， “教授” 识别系统如何将输入矢量映射为输出矢量的过程．
测试样本(testing sample): 指一些类别信息对于分类器未知（不提供给分类器其类别信息）的样本，通常使用它们来测试分类器的性能．
测试集合C testing set): 指测试样本所组成的集合．当测试集合与训练集合没有交集时，称为独立的测试集．
测试(testing): 指将测试样本作为输入送入已训练好的分类器，得到分类结果并对分类正确率进行统计的过程．
识别率(accuracy): 指对于某一样本集合而言，经分类器识别正确的样本占总样本数的比例。
泛化精度(generalization accuracy): 指分类器在独立于训练样本的测试集合上的识别率．

识别问题的一般描述

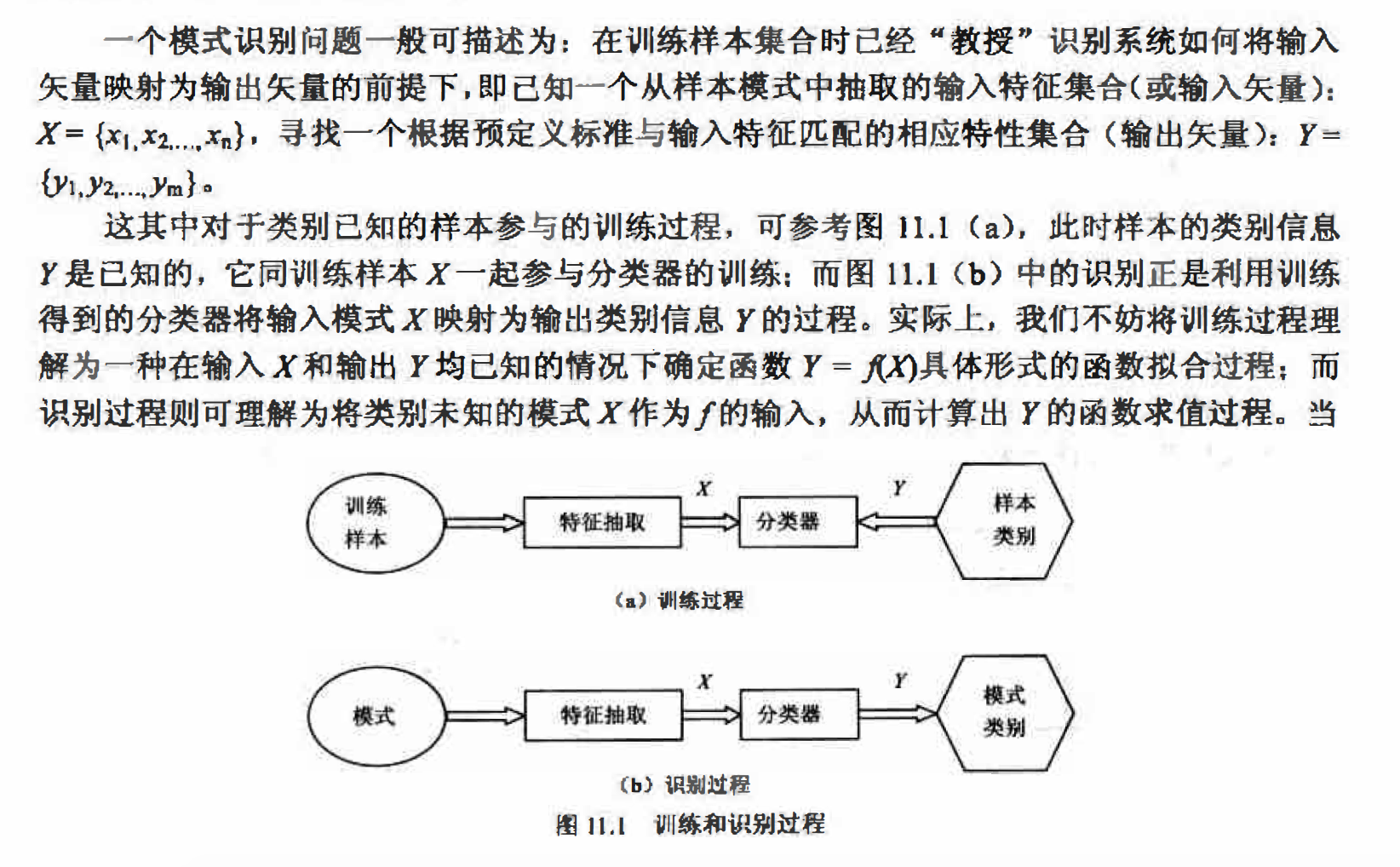
这里的函数f很可能不具有解析形式，有时会相当复杂，它代表着一种广义上的映射关系。
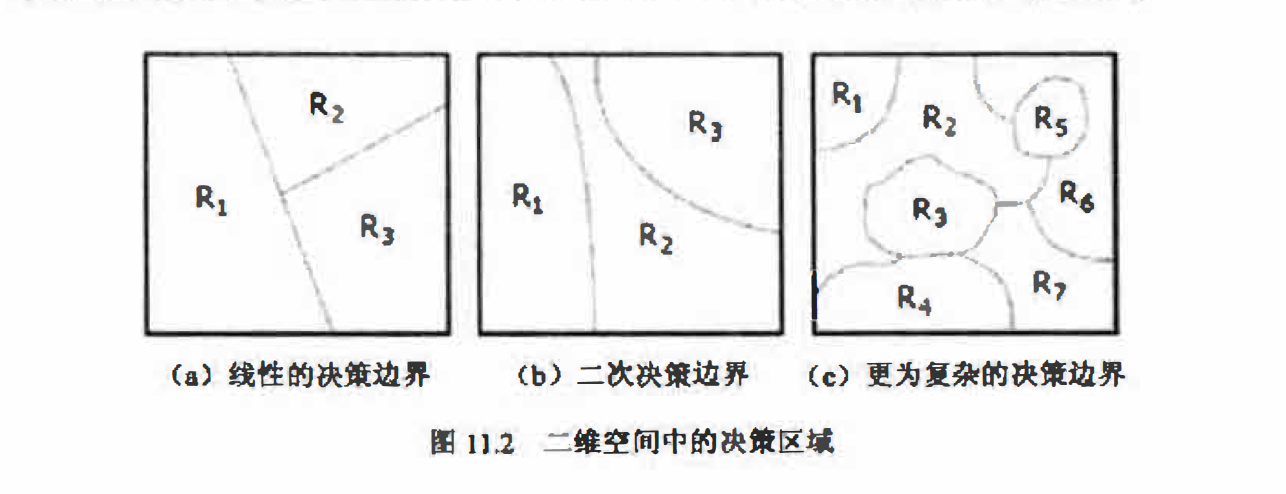
在第10.1.3小节中讨论特征向量及其几何解释时，我们曾指出了识别（分类）的任务就是找到对特征空间的一种合理划分。分类器将特征空间分成标记为类别的决策区域，对于唯一的分类结果，这些区域必须覆盖整个特征空间且不相交，而每个区域的边缘称为决策边界。从这个意义上说分类器就是分割决策区域的决策边界函数集合，图11.2给出了一些典型的决策区域和决策边界。对特征矢量的分类就是确定它属于那个决策区域的过程.

过度拟合(Overlit)

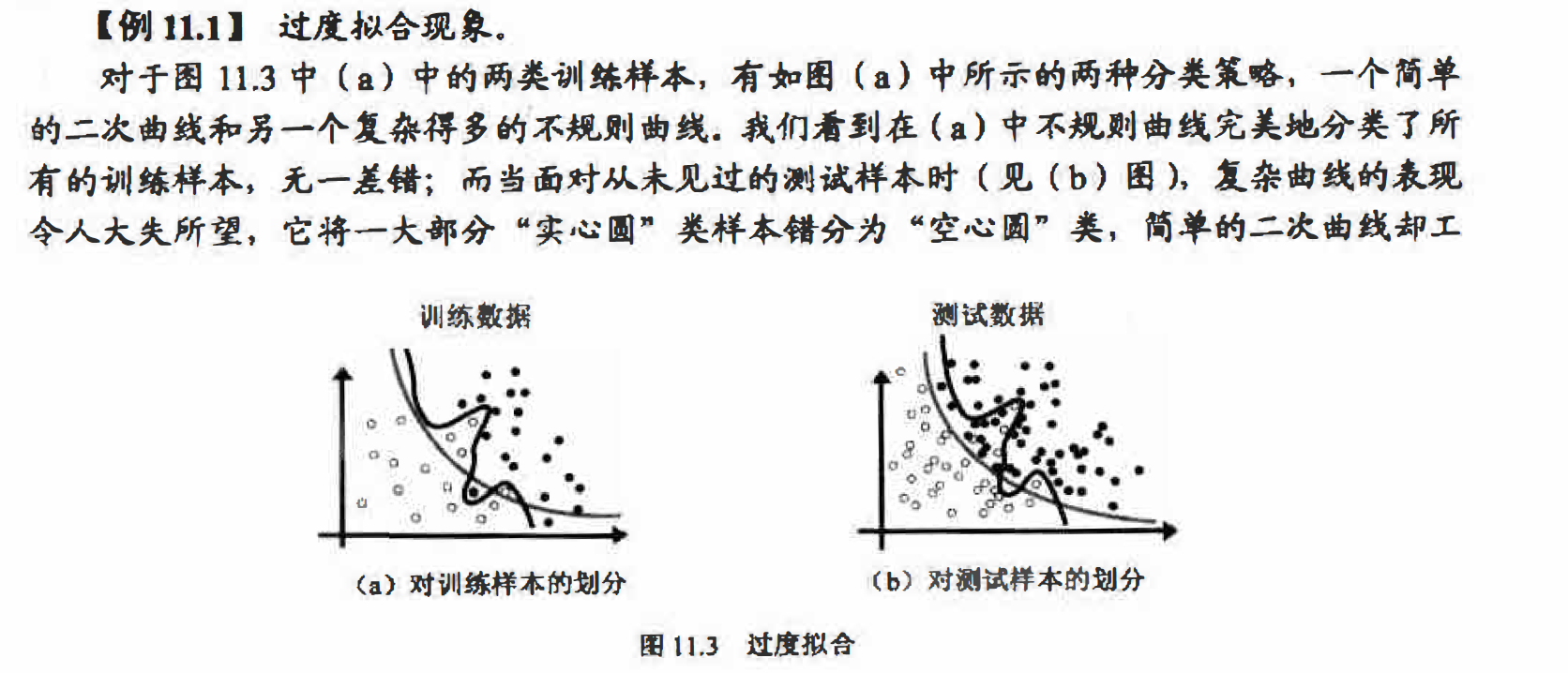作得相当好．究其原因，主要是过度复杂的决策边界不能够对新数据进行很好地归纳（泛化一般化），它们过于倾向对训练数据的正确划分（复杂的形式正好为它们完美地拟合训练数据创造了条件），而不能够对真正的数据模型进行很好地分类．这个问题称为过度拟合(overfit)简单的决策边界对训练数据不够理想，但是对新数据却往往能够较好地归纳．

模式识别系统结构
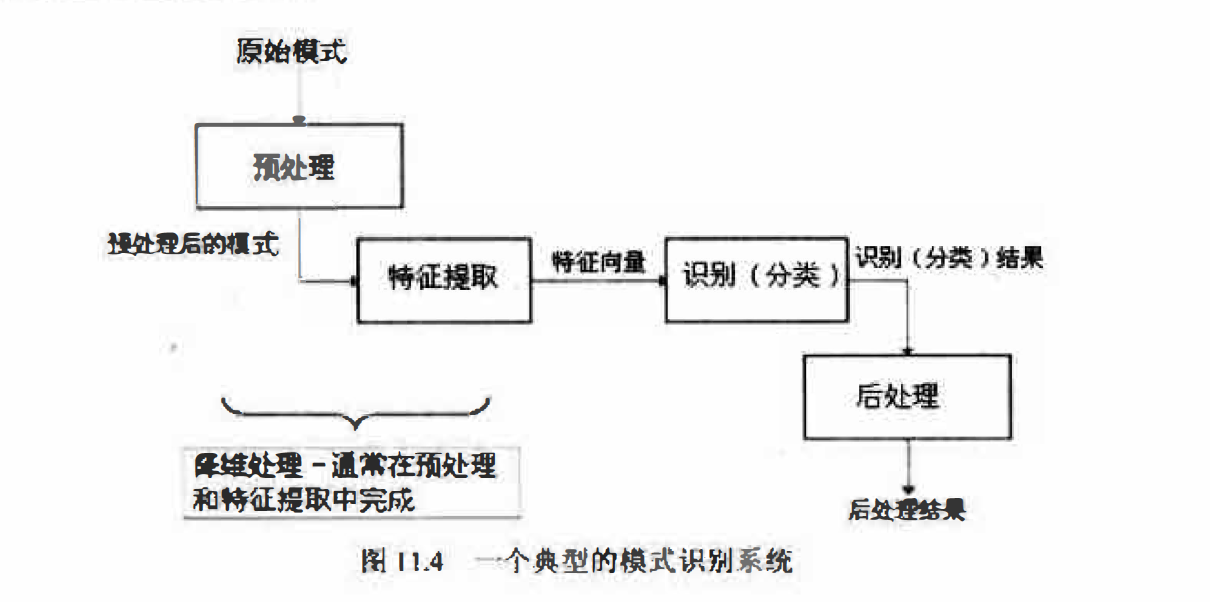
本节最后，图11.4为我们展示了一个典型的模式识别系统的结构。原始模式首先经过预处理（本书的3到9章讨论的都是图像预处理的方法）；而后经过特征提取（第1O章）得到适合分类器处理的特征向量，此过程中有时也包括必要的降维处理；最后分类器输出的识别结果常常还需要后处理。所谓后处理主要指根据得到的识别结果进行评估和改进，像如何调整分类器参数以防止过度拟合等。

训练学习方法分类

一般的训练／学习过程是指在给定一般的模型或分类器形式的情况下，利用训练样本去学习和估计模型的未知参数，具体地说就是用某种算法来降低训练样本的分类误差。比如在第12章人工神经网络中将要学习的梯度下降算法，它通过调节分类器的参数，使训练朝着能够降低误差的方向进行．还有很多其他形式的学习算法，通常可分为以下几种形式：

教师指导的学习：又称为有监督学习。是指在训练样本集中的每个输入样本类别均已知的情况下进行学习，也就是使用训练模式和相应的类别标记一起来” 教授“ 分类器．日常生活中有监督学习的一个例子是教孩子识字，教师将字本身（样本）和具体是什么字（类别）一起教给孩子。
无教师指导的学习：又称为无监督学习．是指在样本中没有相应的类别信息的情况下，系统对输入样本自动形成“自然的” 组织或簇(cluster). 如“ 聚类算法” 就是一种典型的无监督学习.
加强学习：又称为基于评价的学习．在加强学习中，并不把类别信息直接提供给分类器，而是让分类器自己根据输入样本计算输出类别，将它与已知的类别标记进行比较,判断对已知训练模式的分类是否正确，从而辅助分类器的学习。日常生活中加强学习的一个例子是提供正确答案的考试讲评，这里考生就相当于分类器，他们先是进行考试（分类），然后根据教师提供的标准答案来改善知识体系（分类器模型）．

模式识别方法分类

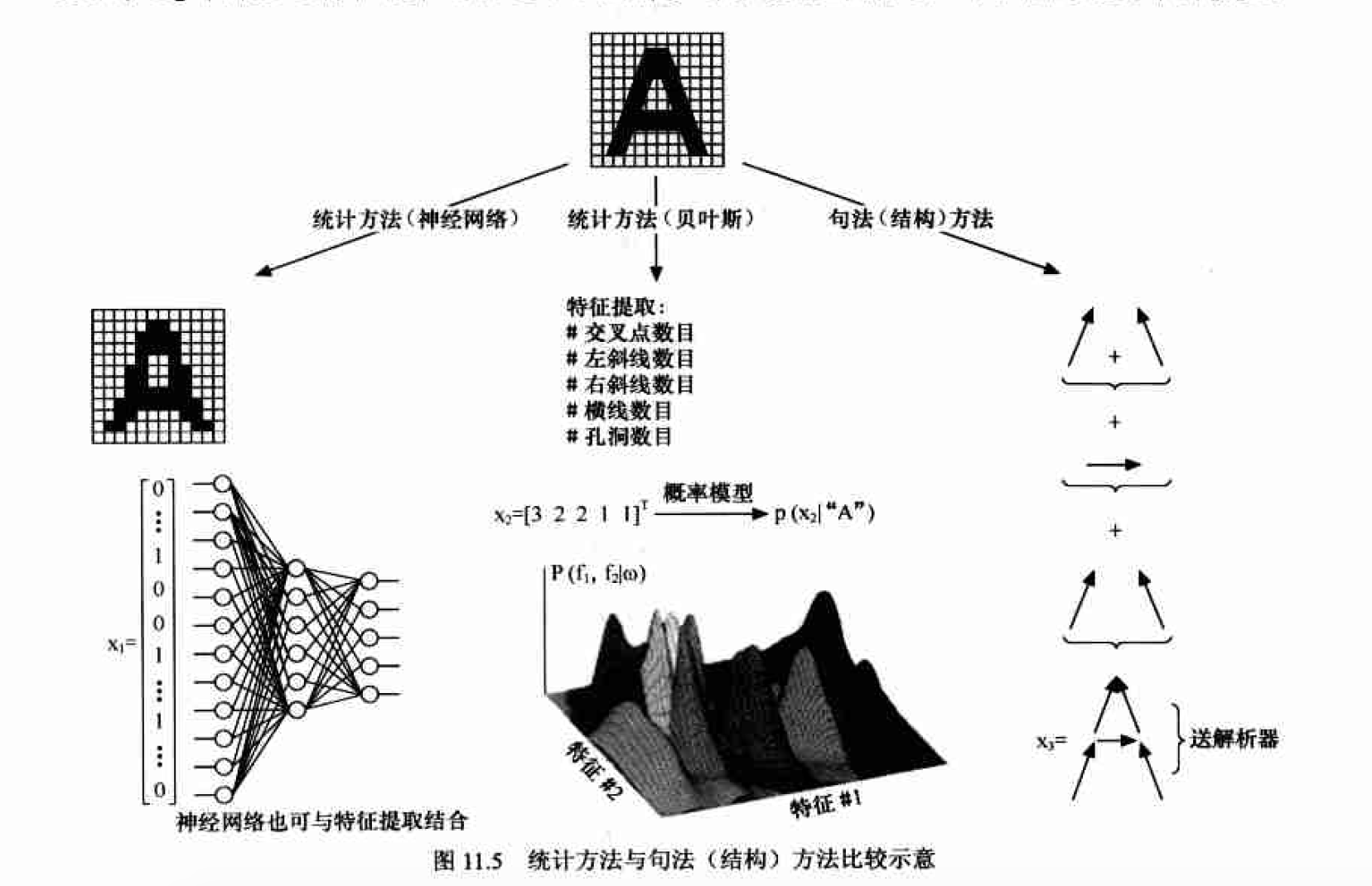
有两种基本的模式识别方法，即统计模式识别(statistical pattern. recognition)方法和句法（结构）模式识别(syntactic pattern recognjtion)方法。统计模式识别是对模式的统计分类方法，即结合统计概率论的贝叶斯决策系统进行模式识别的技术，又称为决策理论识别方法；而利用模式与子模式分层结构的树状信息所完成的模式识别工作，就是句法（结构）模式识别。

统计方法与句法（结构）方法的比较
图11.5给出了对于光学字符识别(OCR)问题统计方法与结构化方法在解决问题上的不同思路．

小结
模式识别方法的选择取决于问题的性质。如果被识别的对象极为复杂，而且包含丰富的结构信息，一般采用句法方法：被识别对象不很复杂或不含明显的结构信息，一般采用统计方法。但是，这两种方法不能截然分开，在句法方法中，基元本身就是用统计方法抽取的。在应用中，将这两种方法结合起来分别施加千不同的层次，常能收到较好的效果。
本书井不是一本专门介绍模式识别的书籍，后续的讨论将不涉及句法模式识别的相关内容，这主要是出于对本书内容完整性和紧凑性的考虑（句法模式以自然语言与自动机为其理论根基）；同时我们也不准备从经典的贝叶斯分类理论开始，对各种统计模式识别技术一一讨论，而是将着眼于目前统计模式识别领域中十分活跃、和图像识别关系密切并且已在工程技术领域获得广泛应用的两种非常实用的分类器技术－一－人工神经网络（第12章）和支持向量机（第13章）。

最小距离分类器和模板匹配

最小距离分类又称最近邻分类，是一种非常简单的分类思想。这种基于匹配的分类技术通过以一种原型模式向量代表每一个类别，识别时一个未知模式被赋予一个按照预先定义的相似性度量与其距离最近的类别，常用的距离度量有欧氏距离，马氏距离等。下面我们以欧氏距离为例讲解最小距离分类器。一种简单的做法是把每个类所有样本的平均向量作为代表该类的原型，则第i类样本的代表向量为：

基于最小距离分类器的鸠尾属植物分类

% 例11.3 利用最小距离分类器分类３种鸢尾属植物
load fisheriris %载入Matlab自带的鸢尾属植物数据集

% 每类的前40个样本用于生成代表该类的模板，后10个作为独立的测试样本
m1 = mean( meas(1:40, :) ); %第1类的前40个样本的平均向量
m2 = mean( meas(51:90, :) ); %第2类的前40个样本的平均向量
m3 = mean( meas(101:140, :) ); %第3类的前40个样本的平均向量

% 测试样本集
Test = [meas(41:50, :); meas(91:100, :); meas(141:150, :)];
% 测试样本集对应的类别标签
classLabel(1:10) = 1;
classLabel(11:20) = 2;
classLabel(21:30) = 3;

% 利用最小距离分类器分类测试样本
class = zeros(1, 30); %类标签
for ii = 1:size(Test, 1)
   d(1) = norm(Test(ii, :) - m1); %与第１类的距离
   d(2) = norm(Test(ii, :) - m2); %与第２类的距离
   d(3) = norm(Test(ii, :) - m3); %与第３类的距离
   
   [minVal class(ii)] = min(d); %计算最小距离并将距离样本最短的类赋给类标签数组 class
end

% 测试最小距离分类器的识别率
nErr = sum(class ~= classLabel);
rate = 1 - nErr / length(class);
strOut = ['识别率为', num2str(rate*100), '%']

基于相关的模板匹配

改进的相关公式实际上计算的是向量a,b之间的夹角余弦值。显然，它只和图案模式本身的形状或纹理有关，与幅值（亮度）无关。

matlab实现

function Icorr = imcorr(I, w)
% function Icorr = imcorr(I, w, )
% 计算图像 I 与子模式 w 的相关响应，并提示最大的响应位置
% 
% Input：I - 原始图像
%        w - 子图像
%
% Output：Icorr - 响应图像

[m, n] = size(I);
[m0, n0] = size(w);

Icorr = zeros(m-m0+1, n-n0+1); %为响应图像分配空间

vecW = double( w(:) ); %按列存储为向量
normW = norm(vecW); %模式图像对应向量的模

for ii = 1:m-m0+1
    for jj = 1:n-n0+1
        subMat = I(ii:ii+m0-1, jj:jj+n0-1);
        vec = double( subMat(:) ); %按列存储为向量
        Icorr(ii, jj) = vec' * vecW / (norm(vec)*normW+eps); %计算当前位置的相关
    end
end

% 找到最大响相应位置
[iMaxRes, jMaxRes] = find(Icorr == max( Icorr(:) ) );
figure, imshow(I);
hold on
for ii = 1:length(iMaxRes)
    plot(jMaxRes(ii), iMaxRes(ii), 'w*');
    plot([jMaxRes(ii), jMaxRes(ii)+n0-1], [iMaxRes(ii), iMaxRes(ii)], 'w-' );
    plot([jMaxRes(ii)+n0-1, jMaxRes(ii)+n0-1], [iMaxRes(ii), iMaxRes(ii)+m0-1], 'w-' );
    plot([jMaxRes(ii), jMaxRes(ii)+n0-1], [iMaxRes(ii)+m0-1, iMaxRes(ii)+m0-1], 'w-' );
    plot([jMaxRes(ii), jMaxRes(ii)], [iMaxRes(ii), iMaxRes(ii)+m0-1], 'w-' );
end

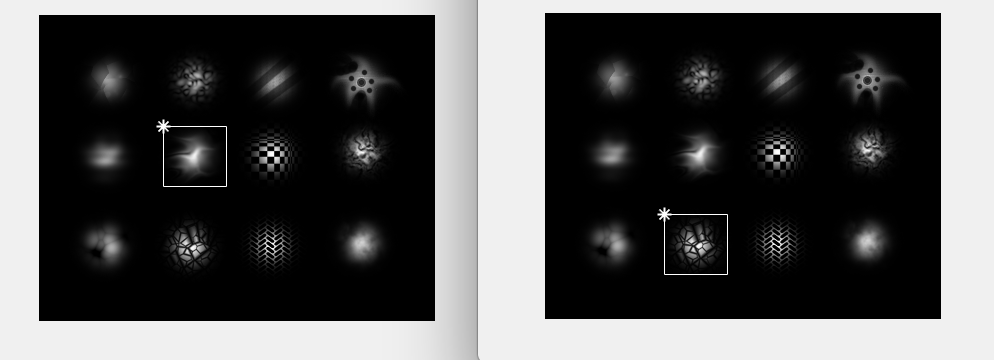
虽然我们之前通过向量模值的归一化得到了幅值（亮度）不变的相关匹配算子，但相关计算仍然对尺寸和旋转变换非常敏感。如果子图像w与图像f中对应的相似目标大小不同，则不能识别，因此因利用不同分辨率来识别。这在计算量上要求很大，因而很难在实际系统中使用。类似的，如果旋转变化的性质是未知的，则寻找最佳匹配就要求对w进行全方位的旋转。更多的时候，我们需要利用对问题的先验知识得到有关尺寸和旋转变换方式的一些线索，从而借助几何变换中的一些技术在匹配之前对这些变换进行归一化处理。

相关匹配的计算效率
一般子图像模式w总是比图像f要小得多。尽管如此，除非w非常小，否则例11.4中采用的空间相关算法的计算量会比较大，以至于总是要依靠硬件来实现。
一种提升计算效率的方法是在频域中实现相关，回忆第6章中曾学习过的卷积定理，它为我们建立了空间卷积和频域乘积之间的对应关系。类似的，通过相关定理可以将空间相关与频域乘积联系起来。相关定理中指出了两个函数的空间相关可以用一个函数的傅立叶变换同另一个函数的傅立叶变换的傅共轭的乘积的傅立叶逆变换得到，当然反过来也成立，即：

function Icorr = dftcorr(I, w)
% function Icorr = dftcorr(I, w)
% 在频域下计算图像 I 与子模式 w 的相关响应，并提示最大的响应位置
% 
% Input：I - 原始图像
%        w - 子图像
%
% Output：Icorr - 响应图像
I = double(I);
[m n] = size(I);
[m0 n0] = size(w);
F = fft2(I);
w = conj(fft2(w, m, n)); %w 频谱的共轭
Ffilt = w .* F; %频域滤波结果
Icorr = real(ifft2(Ffilt)); %反变换回空域


% 找到最响相应位置
[iMaxRes, jMaxRes] = find(Icorr == max( Icorr(:) ) );
figure, imshow(I, []);
hold on
for ii = 1:length(iMaxRes)
    plot(jMaxRes(ii), iMaxRes(ii), 'w*');
    plot([jMaxRes(ii), jMaxRes(ii)+n0-1], [iMaxRes(ii), iMaxRes(ii)], 'w-' );
    plot([jMaxRes(ii)+n0-1, jMaxRes(ii)+n0-1], [iMaxRes(ii), iMaxRes(ii)+m0-1], 'w-' );
    plot([jMaxRes(ii), jMaxRes(ii)+n0-1], [iMaxRes(ii)+m0-1, iMaxRes(ii)+m0-1], 'w-' );
    plot([jMaxRes(ii), jMaxRes(ii)], [iMaxRes(ii), iMaxRes(ii)+m0-1], 'w-' );
end

对千例11.4中的模板匹配问题，和imcorr相比，dftcorr在执行效率上的优势显而易见。这是因为此例中模板图像的大小为61 X64. 虽然比原图像小得多，但已可以说是一个比较大的模板了。文献(Campbell 1969)曾指出，如果w中的非零元素数目小于132 (大约13X13 见方），则直接在空域中计算相关较为划算，否则通过上述方法变换至频域下计算更为合适。当然，这个数目不是绝对的，它还与f的大小以及运算机器本身有关，读者可以把它作为参考，以此决定在应用系统中实现相关的具体方式。