图像处理

图像特征提取

Posted by jjx on January 2, 2017

从本节开始， 我们将逐步从数字图像处理向图像识别过渡。 严格地说， 图像特征提取属于图像分析的范畴， 是数字图像处理的高级阶段， 同时也是图像识别的开始。

本文主要包括以下内容

  • 常用的基本统计特征， 如周长、面积、均值等区域描绘子， 以及直方图和灰度共现矩阵等纹理描绘子
  • 主成份分析(PCA, PrincipaJ Component Analysis)
  • 局部二进制模式(LBP, LocaJ Binary Pattern)
  • 本章的典型案例分析
    • 基于PCA技术的人脸数据集的降维处理

图像特征概述

众所周知，计算机不认识图像,只认识数字。为了使计算机能够“理解”图像，从而具有真正意义上的“视觉”，本章我们将研究如何从图像中提取有用的数据或信息，得到图像的“非图像” 的表示或描述，如数值、向量和符号等。这一过程就是特征提取，而提取出来的这些“非图像”的表示或描述就是特征。有了这些数值或向量形式的特征我们就可以通过训练过程教会计算机如何懂得这些特征， 从而使计算机具有识别图像的本领。

什么是图像特征
特征是某一类对象区别于其他类对象的相应（本质）特点或特性， 或是这些特点和特性的集合。特征是通过测量或处理能够抽取的数据。对于图像而言， 每一幅图像都具有能够区别于其他类图像的自身特征，有些是可以直观地感受到的自然特征，如亮度、边缘、纹理和色彩等；有些则是需要通过变换或处理才能得到的， 如矩、直方图以及主成份等。

特征向量及其几何解释
我们常常将某一类对象的多个或多种特性组合在一起， 形成一个特征向量来代表该类对象，如果只有单个数值特征，则特征向量为一个一维向量，如果是n个特性 的组合，则为一个n维特征向量。该类特征向量常常作为识别系统的输入。实际上，一个n维特征就是位于n维空间中的点，而识别分类的任务就是找到对这个n维空 间的一种划分。
例如要区分3种不同的鸾尾属植物，可以选择其花瓣长度和花瓣宽度作为特征，这样就以1个2维特征代表1个植物对象，比如(5.1,3.5).如果再加上萼片长度和萼片宽度， 则每个鸾尾属植物对象由一个4维特征向置表示， 如(5.1, 3.5.1.4, 0.2)。

特征提取的一般原则
图像识别实际上是一个分类的过程，为了识别出某图像所属的类别，我们需要将它与其他不同类别的图像区分开来。这就要求选取的特征不仅要能够很好地描述图像， 更重要的是还要能够很好地区分不同类别的图像。
我们希望选择那些在同类图像之间差异较小（较小的类内距），在不同类别的图像之间差异较大（较大的类间距）的图像特征， 我们称之为最具有区分能力(most discriminative)的特征。此外， 在特征提取中先验知识扮演着重要的角色， 如何依靠先验知识来帮助我们选择特征也是后面将持续关注的问题。

特征的评价标准
一般来说，特征提取应具体问题具体分析，其评价标准具有一定的主观性。然而，还是有一些可供遵循的普遍原则，能够作为我们在特征提取实践中的指导。总结如下。

  • 特征应当容易提取． 换言之， 为了得到这些特征我们付出的代价不能太大． 当然， 这还要与特征的分类能力权衡考虑．
  • 选取的特征应对噪声和不相关转换不敏感． 比如要识别车牌号码， 车牌照片可能是从各个角度拍摄的， 而我们关心的是车牌上字母和数字的内容， 因此就需要得到对几何失真变形等转换不敏感的描绘子， 从而得到旋转不变， 或是投影失真不变的特征．
  • 最重要的一点， 总是应试图寻找最具区分能力的特征．

基本统计特征

本节将主要介绍一些常用的基本统计特征， 包括一些简单的区域描绘子， 直方图及其统计特征， 以及灰度共现矩阵等.

简单的区域描绘子及其Matlab实现

在经过图像分割得到各种我们感兴趣的区域之后，可以利用下面介绍的一些简单区域描绘子作为代表该区域的特征。通常将这些区域特征组合成特征向量以供分类使用。

常用的简单区域描绘子如下。

  • 周长：区域边界的长度， 即位于区域边界上的像素数目．
  • 面积：， 区域中的像素总数．
  • 致密性：（周长） 2/面积．
  • 区域的质心．
  • 灰度均值： 区域中所有像素的平均值．
  • 灰度中值： 区域中所有像素的排序中值．
  • 包含区域的最小矩形．
  • 最小或最大灰度级．
  • 大于或小于均值的像素数．
  • 欧拉数： 区域中的对象数减去这些对象的孔洞数。

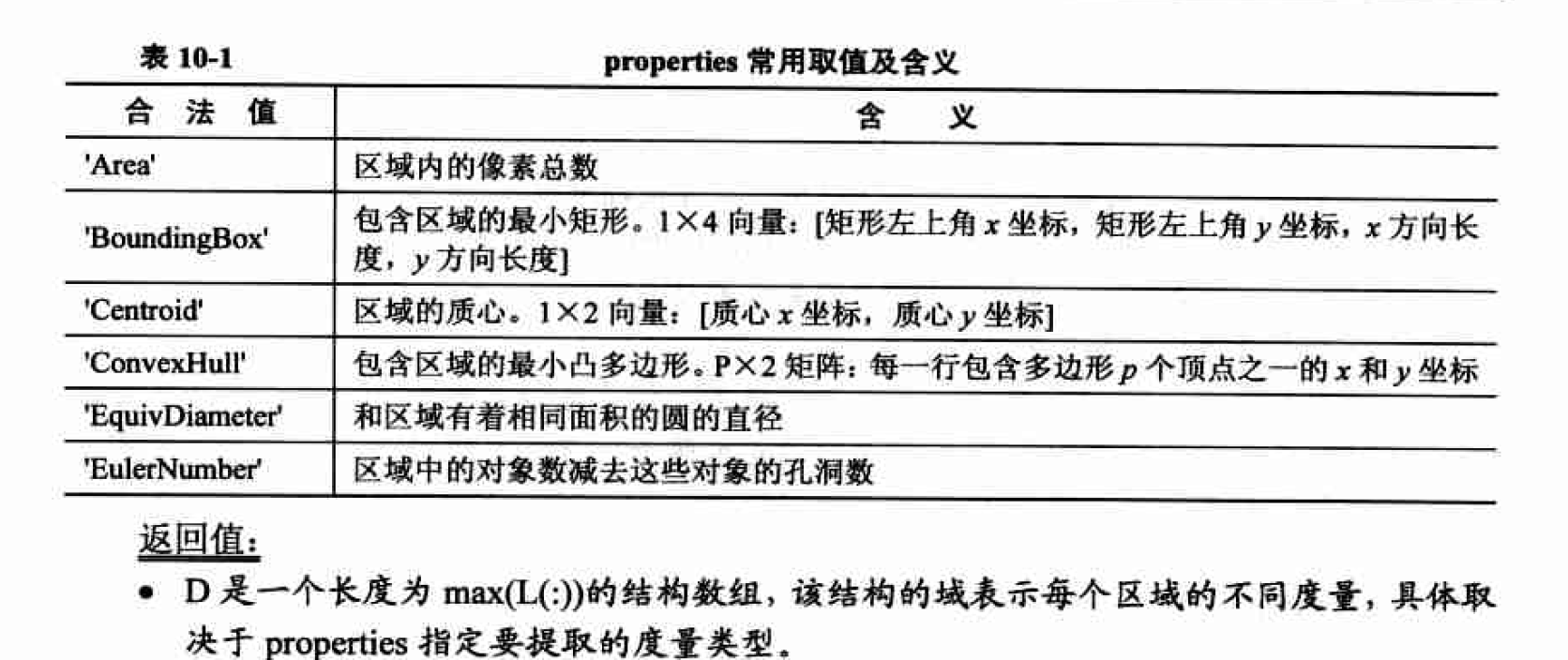
在Matlab中， 函数regionprops用于计算区域描绘子的有利工具， 其原型为：
D = regionprops(L,properties)
L是一个标记矩阵， 可通过8.3.4小节介绍的连通区标注函数bwlabel得到．
properties可以是一个用逗号分割的字符串列表， 其一些常用取值如表10.1所示

利用regionprops函数提取简单的区域特征

I = imread('bw_mouth.bmp');
I1 = bwlabel(I);
D = regionprops(I1,'area','centroid');
D.Area

直方图及其统计特征

首先来看纹理的概念。纹理是图像固有的特征之一，是灰度（对彩色图像而言是颜色）在空间以一定的形式变换而产生的图案（模式），有时具有一定的周期性。既然纹理区域的像素灰度级分布具有一定的形式，而直方图正是描述图像中像素灰度级分布的有力工具， 因此用直方图来描述纹理就顺理成章了。

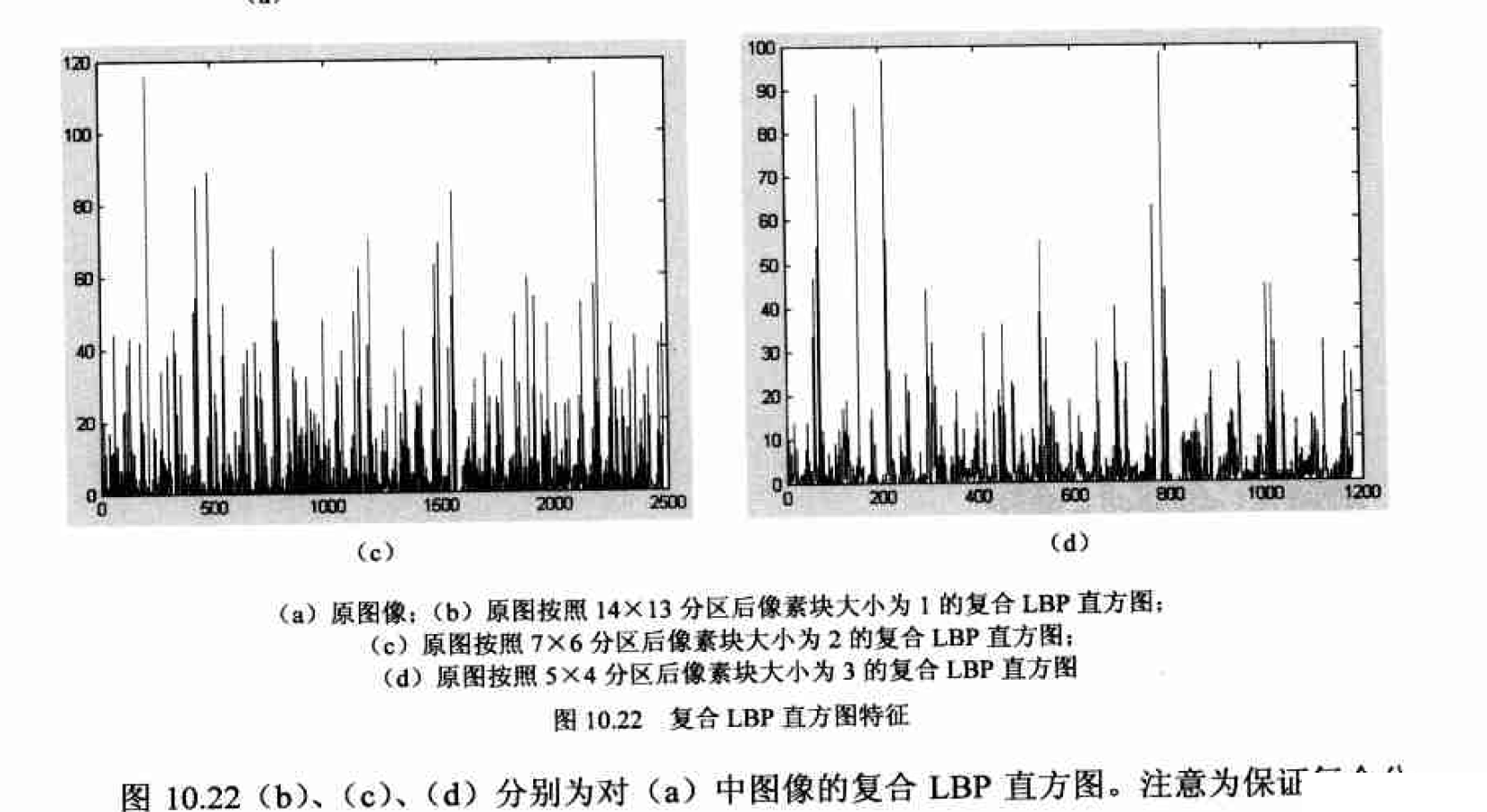
毫无疑问，相似的纹理具有相似的直方图；而由图10.2可见，3种不同特点的纹理对应3种不同的直方图。这说明直方图与纹理之间存在着一定的对应关系。因此，我们可以用直 方图或其统计特征作为图像纹理特征。直方图本身就是一个向量，向量的维数是直方图统计 的灰度级数，因此我们可以直接以此向量作为代表图像纹理的样本特征向量，从而交给分类器处理，对于LBP直方图就常常这样处理（见10.5节）；另一种思路是进一步从直方图中提取出能够很好地描述直方图的统计特征，将直方图的这些统计特征组合成为样本特征向量， 这样做可以大大降低特征向量的维数。

直方图的常用统计特征如下所述。
一个由均值、标准差、平滑度和熵组合而成的特征向量如：v = (m,a, R, e)。
应认识到直方图及其统计特征是一种区分能力相对较弱的特征，这主要因为直方图属于一阶统计特征，而它们的一阶统计特征是无法反映纹理结构的变化的。直方图与纹理的对应关系并不是一对一的：首先，不同的纹理可能具有相同或相似的直方图，如图10.3所示的两种截然不同的图案就具有完全相同的直方图；其次，即便是两个不同的直方m.也可能具有相同的统计特 征如均值、标准差等。因此，依靠直方图及其统计特征来作为分类特征时需要特别注意。

灰度共现矩阵

我们说灰度直方图是一种描述单个像素灰度分布的一阶统计量；而灰度共现矩阵描述的则是具有某种空间位置关系的两个像素的联合分布，可以看成是两个像素灰度对的联合直方图，是种二阶统计量。

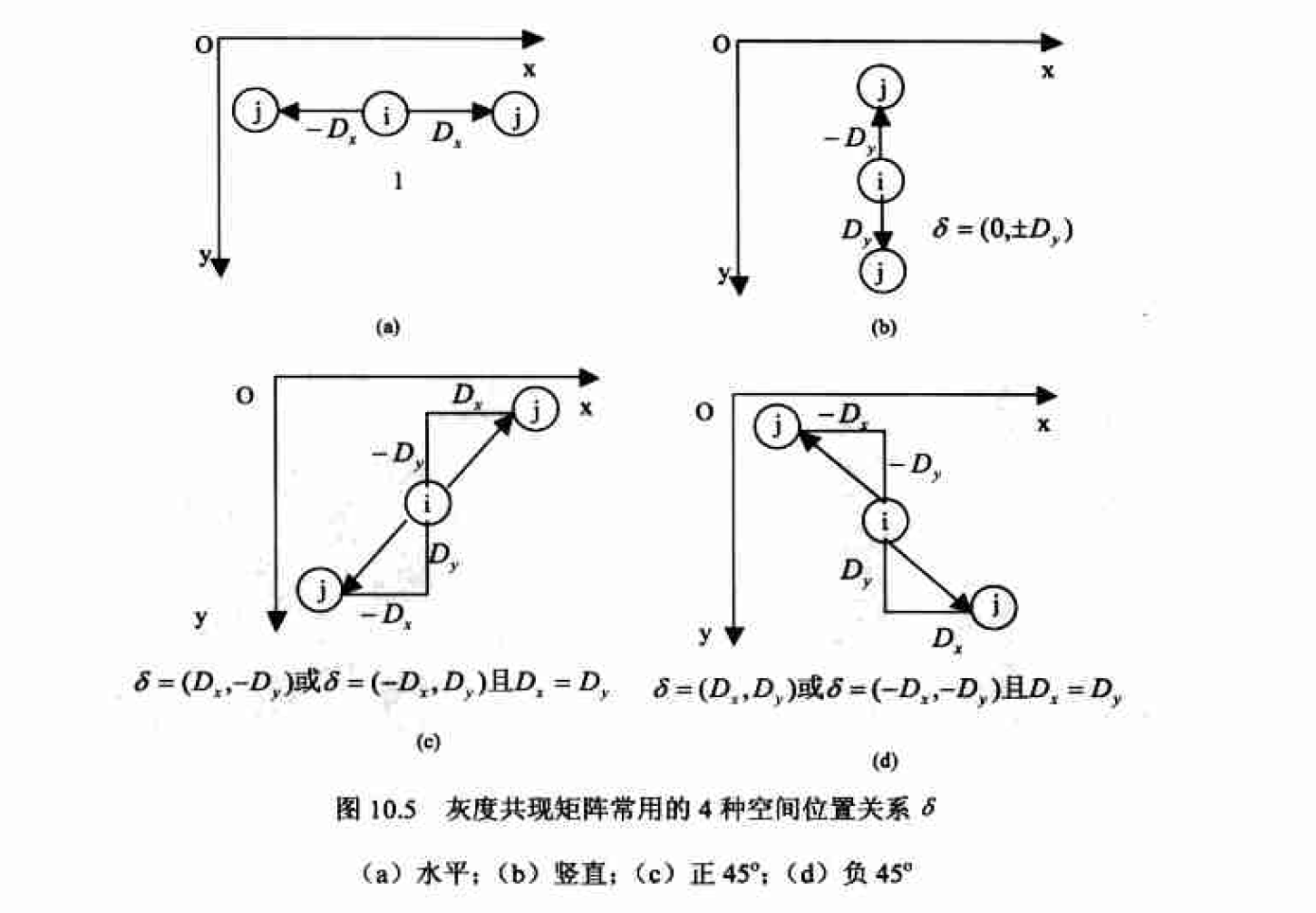
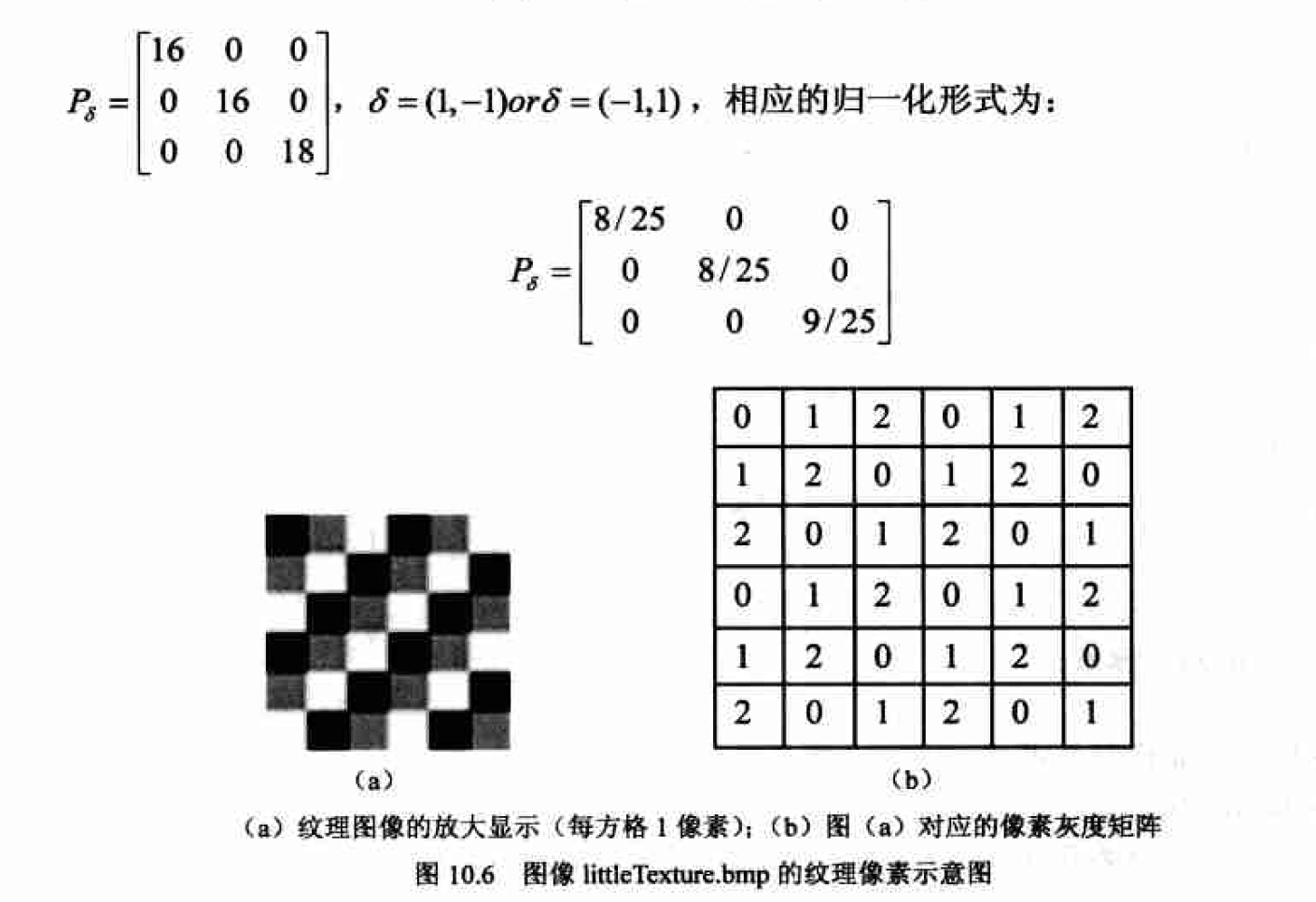由于灰度共现矩阵总共含有LXL个元素，当灰度级L比较大时它将是一个庞大的方阵。如对于一般的256灰度图，凡就是一个256X256的矩阵，共$2^16$ 个元素。如此庞大的矩阵将使后续的计算量剧增。因此普通灰度图像通常要经过处理以减少灰度级数，而后再计算灰度共现矩阵。可以通过分析纹理图像的直方图，在尽量不影响纹理质量的情况下．通过适当的灰度变换来达到灰度级压缩的目的。

特征降维

维度灾难
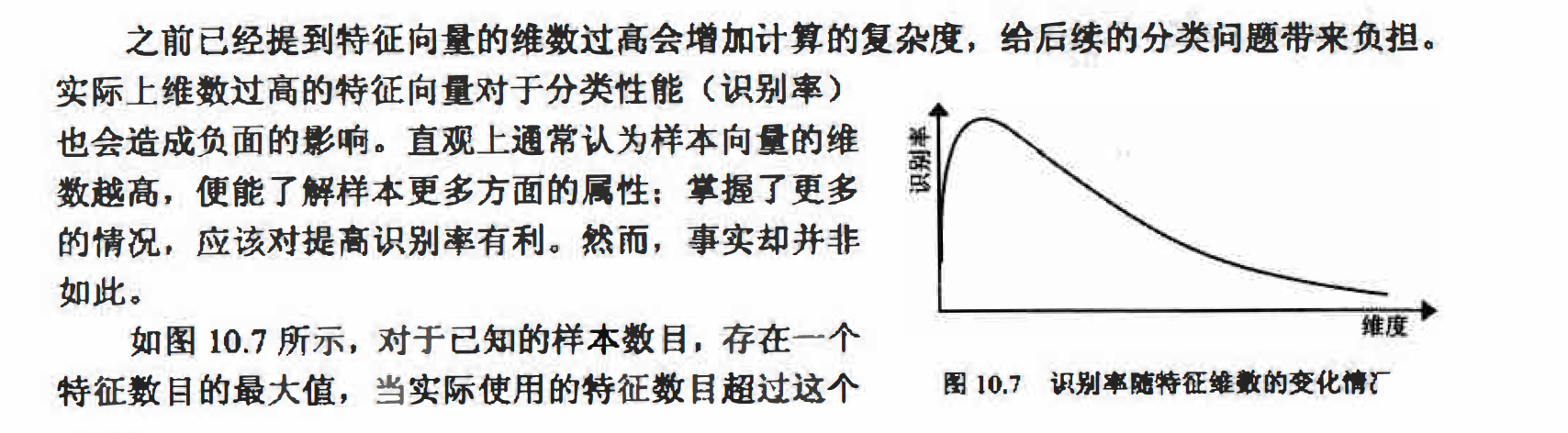最大值时，分类器的性能不是得到改善，而是退化。这种现象正是在模式识别中被称为“维度灾难”的一种表现形式。例如，我们要区分西瓜和冬瓜，表皮的纹理和长宽比例都是很好 的特征，还可以再加上瓜籽的颜色以辅助判断，然而继续加入重量、体积等特征可能是无益 的，甚至还会对分类造成干扰。
基于以上所述原因，降维对我们产生了巨大的吸引力。在低维空间中计算和分类都将变 得简单很多，训练（教授分类器如何区分不同类样本的过程，详见第11章）所需的样本数目也会大大降低。通过选择好的特征，摒弃坏的特征(10.3.2特征选择），将有助于分类器性能的提升；在通过组合特征降维时，在绝大多数情况下，丢弃某些特征所损失的信息通过在低 维空间中更加精确的映射(10.3.3特征抽取）可以得到补偿。

具体来说，降低维度又存在着两种方法：特征选择和特征抽取。如图10.8所示，特征选择是指选择全部特征的一个子集作为特征向量：特征抽取是指通过已有特征的组合建立一个 新的特征子集，10.3.2小节将要介绍的主成份分析方法(principa1component analysis, PCA)就是通过原特征的线性组合建立新的特征子集的一种特征抽取方法。

特征选择简介

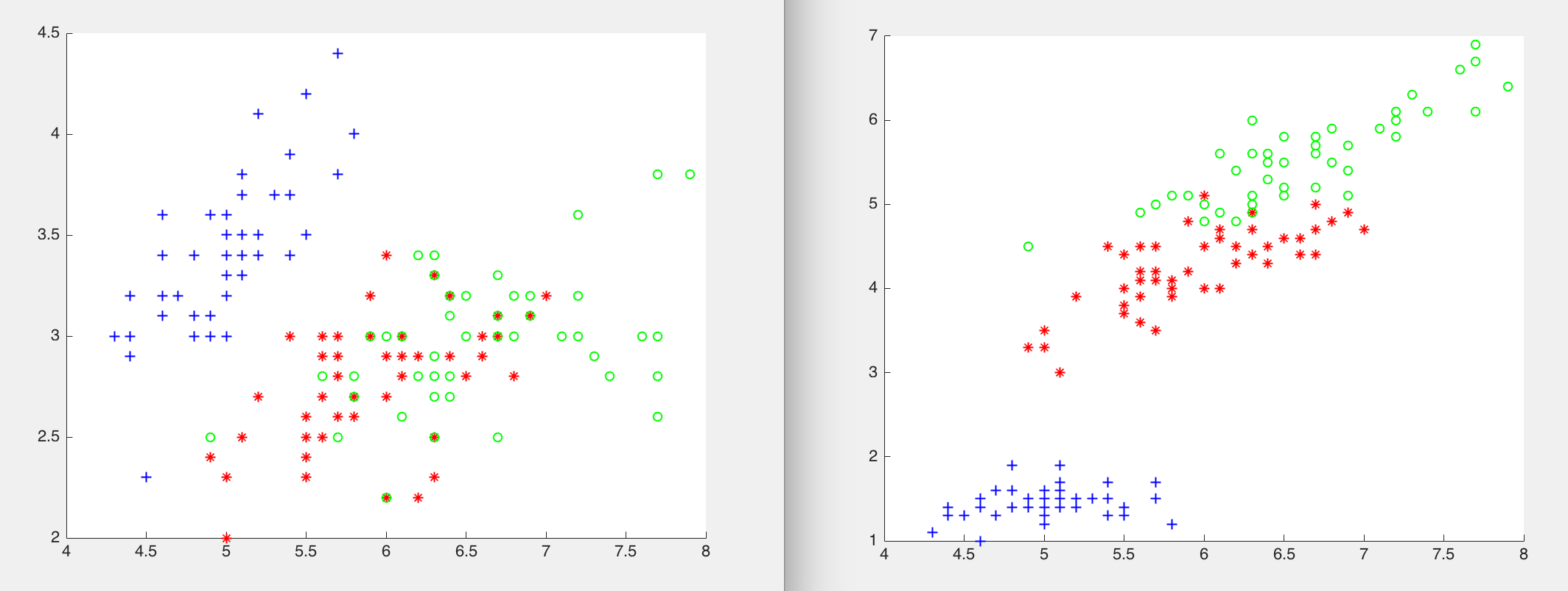
重新回到10.1.3小节那个鸾尾属植物的问题。对于每一个莺尾属植物样本，总共有4个属性可以使用一一花瓣长度、花瓣宽度、萼片长度和萼片宽度。我们的目的是从中选择两个属性组成特征向量用于分类这3种鸾尾属植物。下面的Matlab程序选择了不同的特征子集，并给出了在对应特征空间中样本分布的可视化表示。

load fisheriris;
data = [meas(:,1),meas(:,2)];
figure;
scatter(data(1:50,1),data(1:50,2),'b+');
hold on,scatter(data(51:100,1),data(51:100,2),'r*');
hold on,scatter(data(101:150,1),data(101:150,2),'go');

data = [meas(:,1),meas(:,3)];
figure;
scatter(data(1:50,1),data(1:50,2),'b+');
hold on,scatter(data(51:100,1),data(51:100,2),'r*');
hold on,scatter(data(101:150,1),data(101:150,2),'go');

主成分分析(Princjpal Component Analysis, PCA)

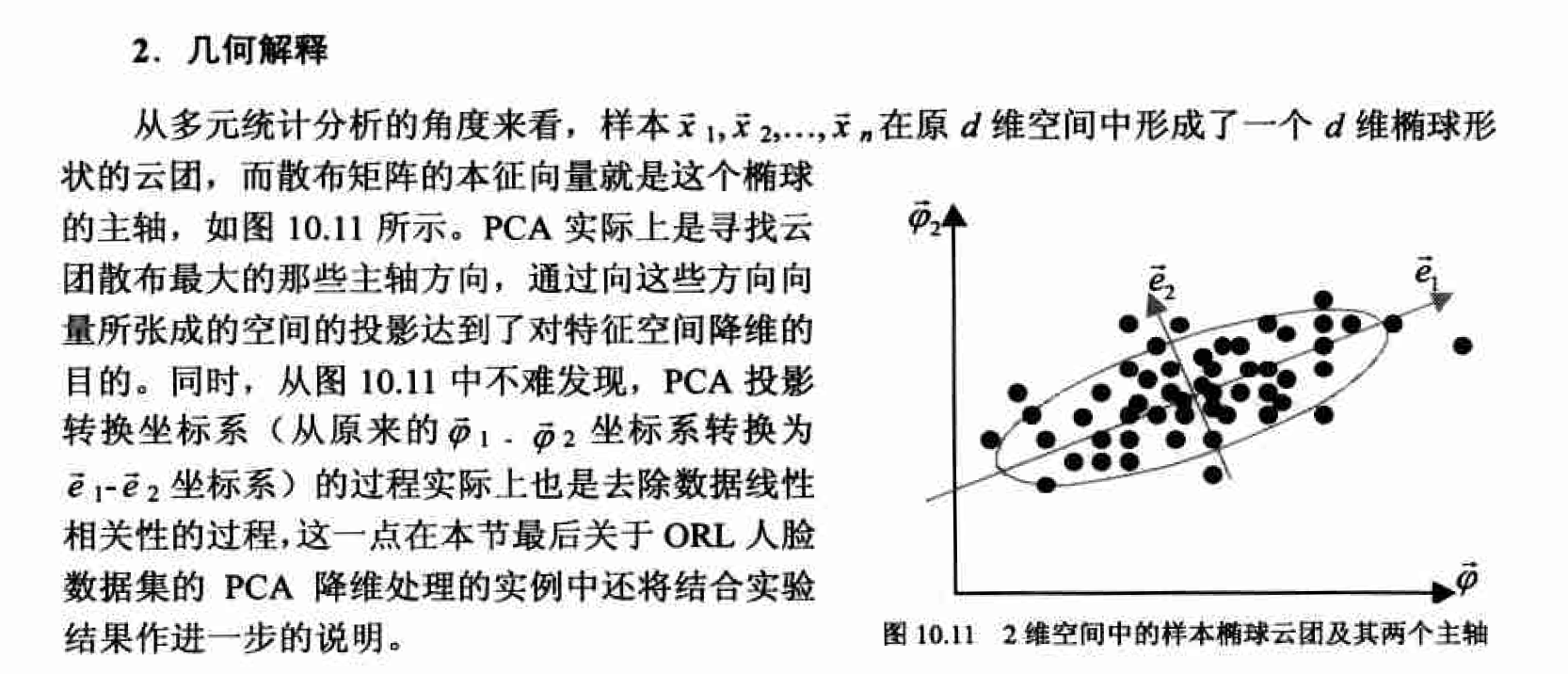
特征抽取是指通过已有特征的组合（变换）建立一个新的特征子集。在众多的组合方法当中，线性组合（变换）因其计算简单且便于解析分析的特点而显得颇具吸引力。下面就介绍一种通过特征的线性组合来实现降维的方法——主成分分析(principal conponent analysis.PCA)。PCA的实质就是在尽可能好地代表原始数据的前提下， 通过线性变换将高维空间中的样本数据投影到低维空间中

具体可参见：降维算法学习
为得到最小平方误差，应选取散布矩阵s的最大本征值所对应的本征向量作为投影直线e的方向。
也就是说， 通过将全部n个样本向 以散布矩阵最大本征值对应的本征向量为方向的直线投影， 可以得到最小平方误差意义下这 n个样本的一维表示。

PCA计算实例

数据表示与数据分类
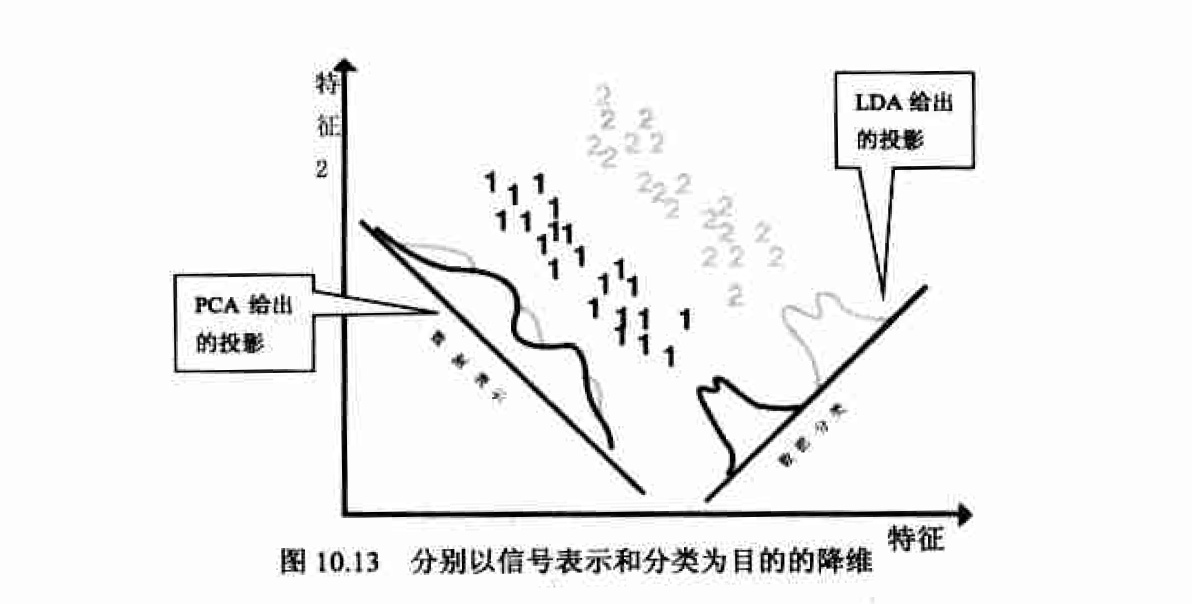
通过PCA降维后的数据并不一定最有利于分类，因为PCA的目的是在低维空间中尽可能好地表示原数据，确切地说是在最小均方差意义下最能代表原始数据。而这一目的有时会和数据分类的初衷相违背。图10.13说明了这种情况，PCA投影后数据样本得到了最小均方意义 下的最好保留 ， 但在降维后的一维空间中两类样本变得非常难以区分。图中还给出了一种适合于分类的投影方案，对应着另一种常用的降维方法-线性判别分析(linear discriminant analysis. LDA)。PCA寻找的是能够有效表示数据的主轴方向，而LDA则是寻找用来有效分类的投影方向。

PCA的Matlab实现
函数princomp实现了对PCA的封装， 其常见调用形式为：
[COEFF,SCORE,latent]= princomp(X);
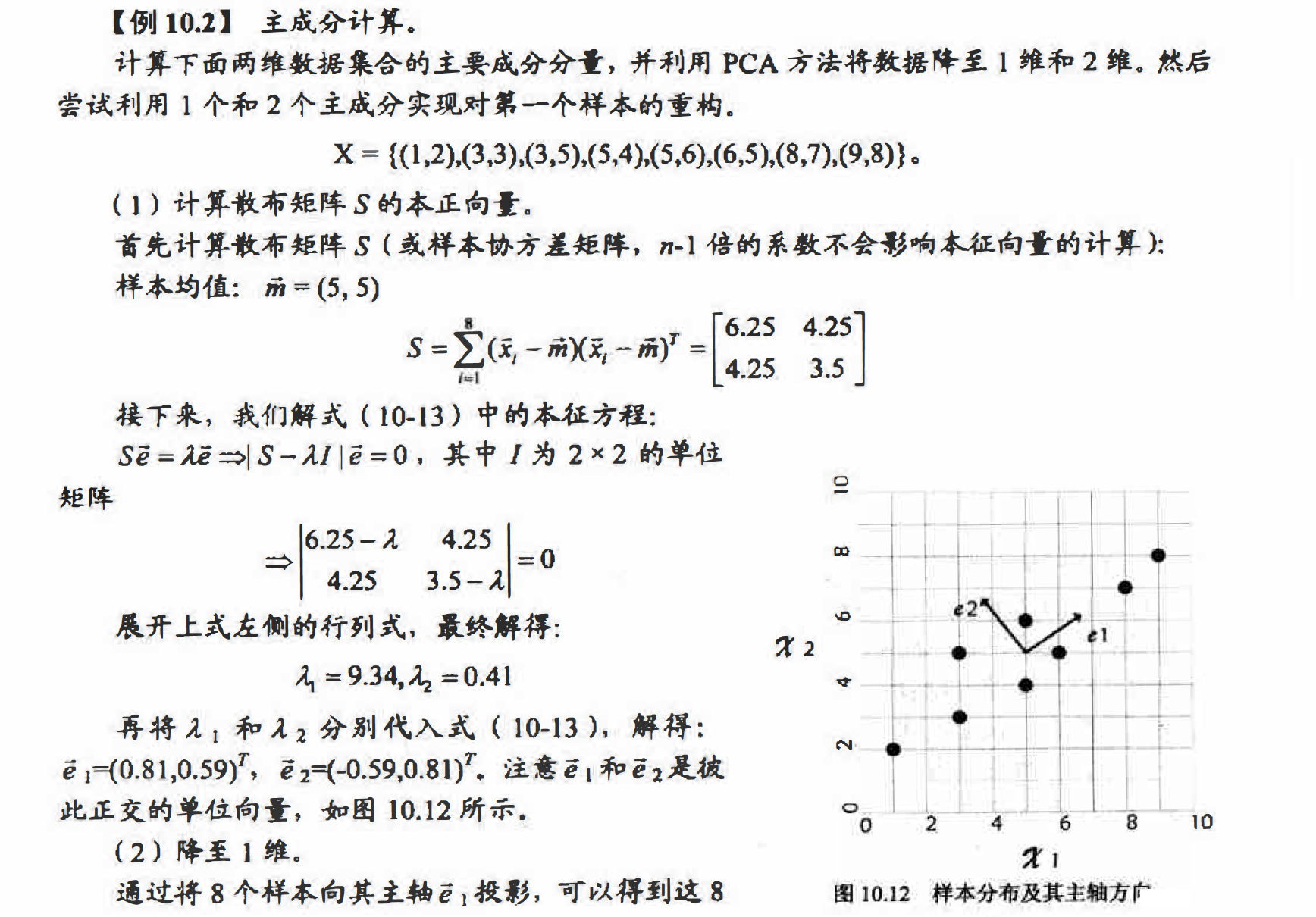
X为原始样本组成nd的矩阵，其每一行是一个样本特征向量，每一列表示样本特征向量的一维．如对于例10.2中的问题，X就是一个82的样本矩阵， 总共8个样本， 每个样本2维．
COEFF: 主成份分量， 即变换空间中的那些基向量, 也是样本协方差矩阵的本征向量．
SCORE: 主成份，X的低维表示， 即X中的数据在主成分分量上的投影（可根据需要取前面几列的).
latent: 一个包含着样本协方差矩阵本征值的向量．

快速PCA及其实现
PCA的计算中最主要的工作量是计算样本协方差矩阵的本征值和本征向量。设样本矩阵 X大小为nd (n个d维样本特征向量）， 则样本散布矩阵（协方差矩阵） S将是一个dXd的方阵，故当维数d较大时计算复杂度会非常高。例如当维数d=1OOOO,S是一个1000010000的矩阵，此时如果采用上面的princomp函数计算主成分，Matlab通常会出现内存耗尽的错误，即使有足够多的内存， 要得到S的全部本征值可能也要花费数小时的时间

Matlab实现
我们编写了fastPCA函数用来对样本矩阵A进行快速主成份分析和降维（降至k维），其输出pcaA为降维后的K维样本特征向量组成的矩阵， 每行一个样本， 列数K为降维后的样本特征维数，相当千princomp函数中的输出SCORE, 而输出V为主成份分量,好princomp函数中的COEFF

function [pcaA V] = fastPCA( A, k )
% 快速PCA
%
% 输入：A --- 样本矩阵，每行为一个样本
%      k --- 降维至 k 维
%
% 输出：pcaA --- 降维后的 k 维样本特征向量组成的矩阵，每行一个样本，列数 k 为降维后的样本特征维数
%      V --- 主成分向量

[r c] = size(A);

% 样本均值
meanVec = mean(A);

% 计算协方差矩阵的转置 covMatT
Z = (A-repmat(meanVec, r, 1));
covMatT = Z * Z';

% 计算 covMatT 的前 k 个本征值和本征向量
[V D] = eigs(covMatT, k);

% 得到协方差矩阵 (covMatT)' 的本征向量
V = Z' * V;

% 本征向量归一化为单位本征向量
for i=1:k
    V(:,i)=V(:,i)/norm(V(:,i));
end

% 线性变换（投影）降维至 k 维
pcaA = Z * V;

% 保存变换矩阵 V 和变换原点 meanVec
save('Mat/PCA.mat', 'V', 'meanVec');

在得到包含R的特征向量的矩阵V之后，为计算散布矩阵S的本征向量，只需计算Z*V。此外，还应注意PCA中需要的是具有单位长度的本征向量， 故最后要除以该向量的模从而将正交本征向量归一化为单位正交本征向量。

局部二进制模式

局部二进制模式(local binary patterns, LBP)最早是作为一种有效的纹理描述算子提出的,由于其对图像局部纹理特征的卓越描绘能力而获得了广泛的应用。LBP特征具有很强的 分类能力(highly discriminative)、较高的计算效率， 并且对于单调的灰度变化具有不变性。

基本LBP

LBP的主要思想是以某一点与其邻域像素的相对灰度作为响应， 正是这种相对机制使 LBP算子对于单调的灰度变化具有不变性。 人脸图像常常会受到光照因素的影响而产生灰度变化，但在一个局部区域内，这种变化常常可以被视为是单调的，因此LBP在光照不均的人 脸识别应用中也取得了很好的效果.

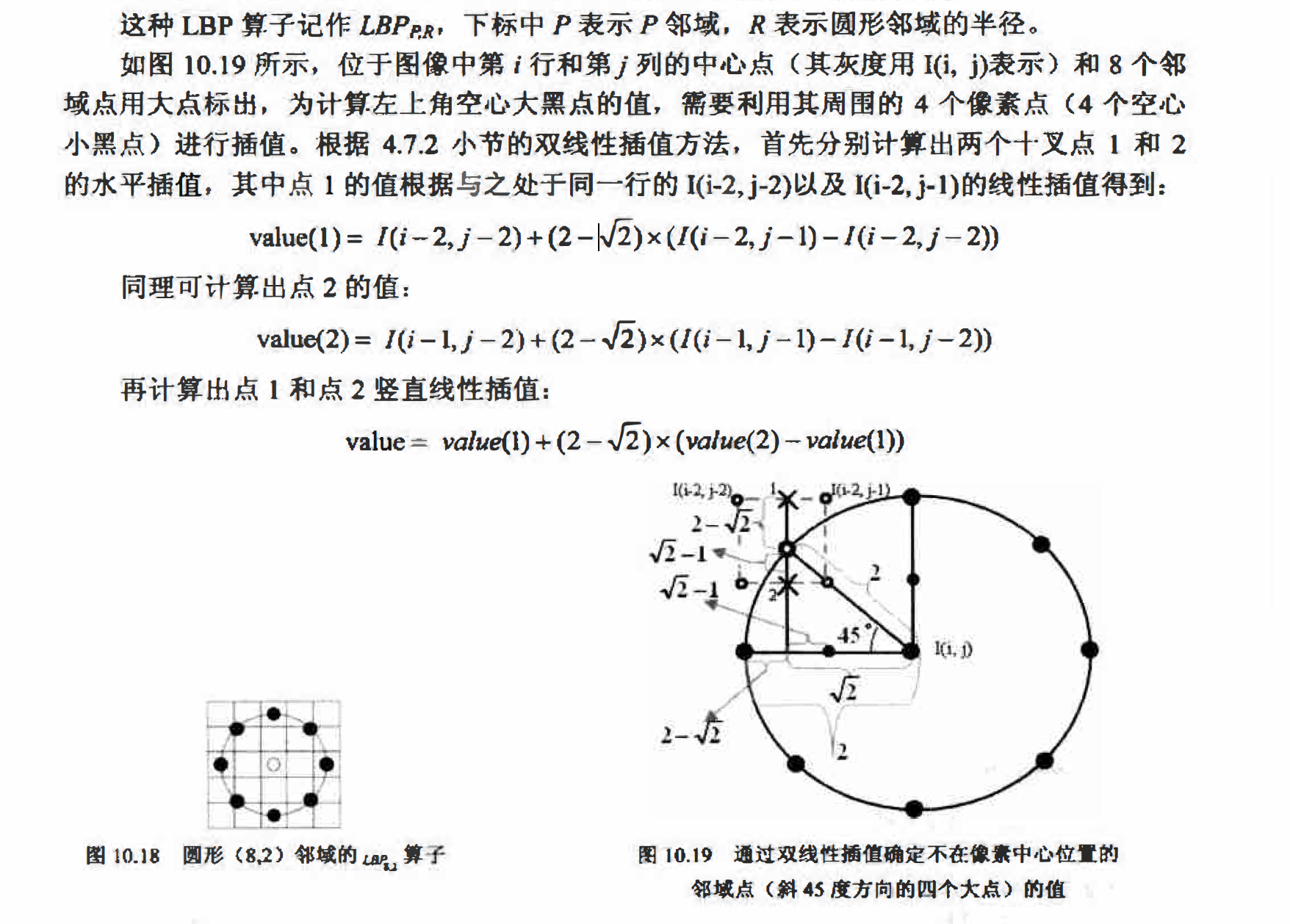
圆形邻域的$LBP_{P,R}$算子

基本LBP算子可以被进一步推广为使用不同大小和形状的邻域。采用圆形的邻域并结合双线性插值运算使我们能够获得任意半径和任意数目的邻域像素点。图10.18给出了一个半径为2的8邻域像素的圆形邻域， 图中每个方格对应一个像素，对于正好处于方格中心的邻 域点（左、上、右、下四个黑点），直接以该点所在方格的像素值作为它的值；对于不在像素中心位置的邻域点（斜45度方向的4个黑点）， 通过双线性插值确定其值。

统一化LBP算子一一UnifomLBP

由于LBP直方图大多都是针对图像中的各个分区分别计算的（详见10.5.5),对于一个普通大小的分块区域，标准LBP算子得到的二进模式数目(LBP直方图收集箱数目）较多，而实际位于该分块区域中的像素数目却相对较少， 这将会得到一个过于稀疏的直方图。从而 使直方图失去统计意义。 因此应设法减少一些冗余的LBP模式， 同时又保留足够的具有重要描绘能力的模式。

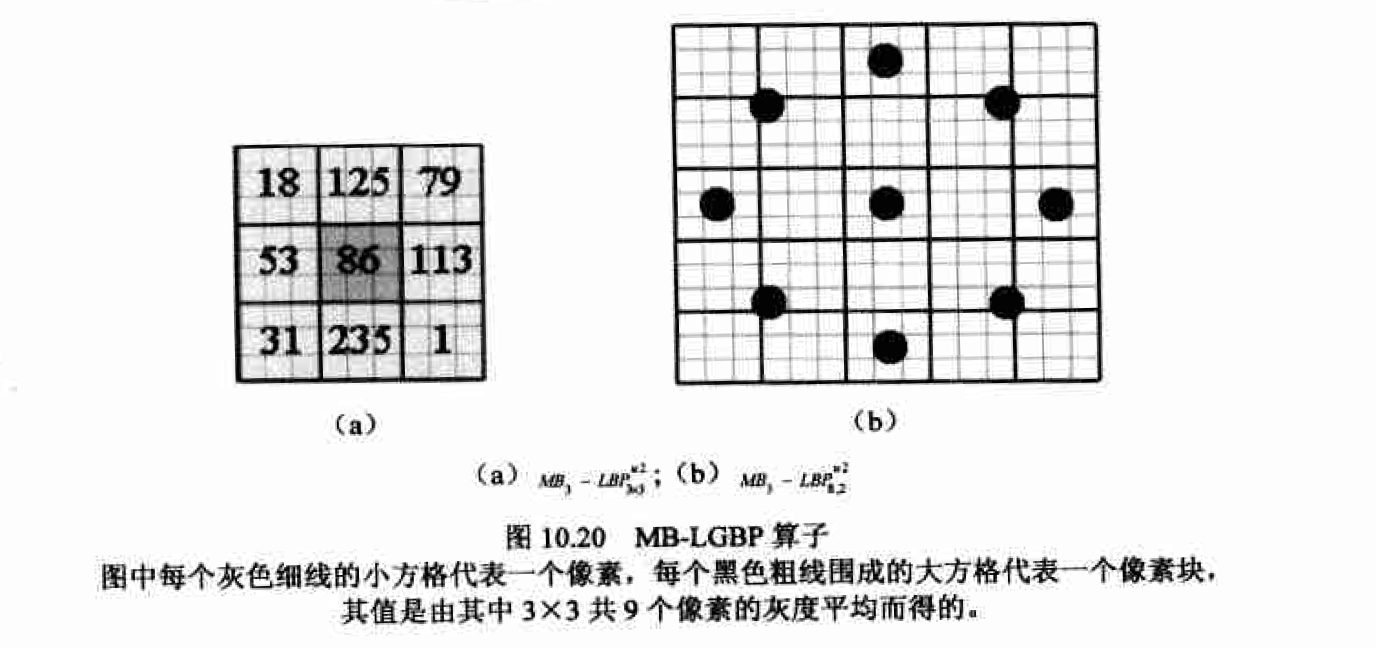
MB-LBP

图像分区

曾提到， 作为图像的一阶统计特征，直方图无法描述图像的结构信息。而图像各个区域的局部特征往往差异较大，如果仅对整个团像的生成一个LBP直方图，这些局部的差异信息就会丢失。分区LBP特征可有效解决这一问题。
具体的方法是将一幅图像适当地划分为PXQ个分区(partition),然后分别计算每个图像分区的直方图特征，最后再将所有块的直方图特征连接成一个复合的特征向量(composite feature)作为代表整个图像的LBP直方图特征。

分区大小的选择 理论上， 越小越精细的分区意味着更好的局部描述能力，但同时会产生更高维数的复合特征。然而过小的分区会造成宜方图过于稀疏从而失去统计意义。人脸识别的应用中选择了18X21的分区大小，这可以作为对于一般问题的指导性标准，因为它是一个精确描述能力与特征复杂度的良好折中。在表情识别中更小一些（如1OX15)的分区被我们证明能够获得更好的分类能力。这里分区大小的单位是.MB-LBP的像素块(block)。如对于传统LBP, 每个 分区大小取18像素X21像素， 则对于应MB-LBP分区大小应取18像素块X21像素块= 54像素X63像素口