形态学图像处理(二)

本文主要包括以下内容

• 二值形态学的经典应用， 细化和像素化， 以及凸壳
• 灰度图像的形态学运算， 包括灰度腐蚀、灰度膨胀、灰度开和灰度闭
• 本章的典型案例分析
  • 在人脸局部图像中定位嘴的中心
  • 显微镜下图像的细菌计数
  • 利用顶帽变换（top-hat）技术解决光照不均问题

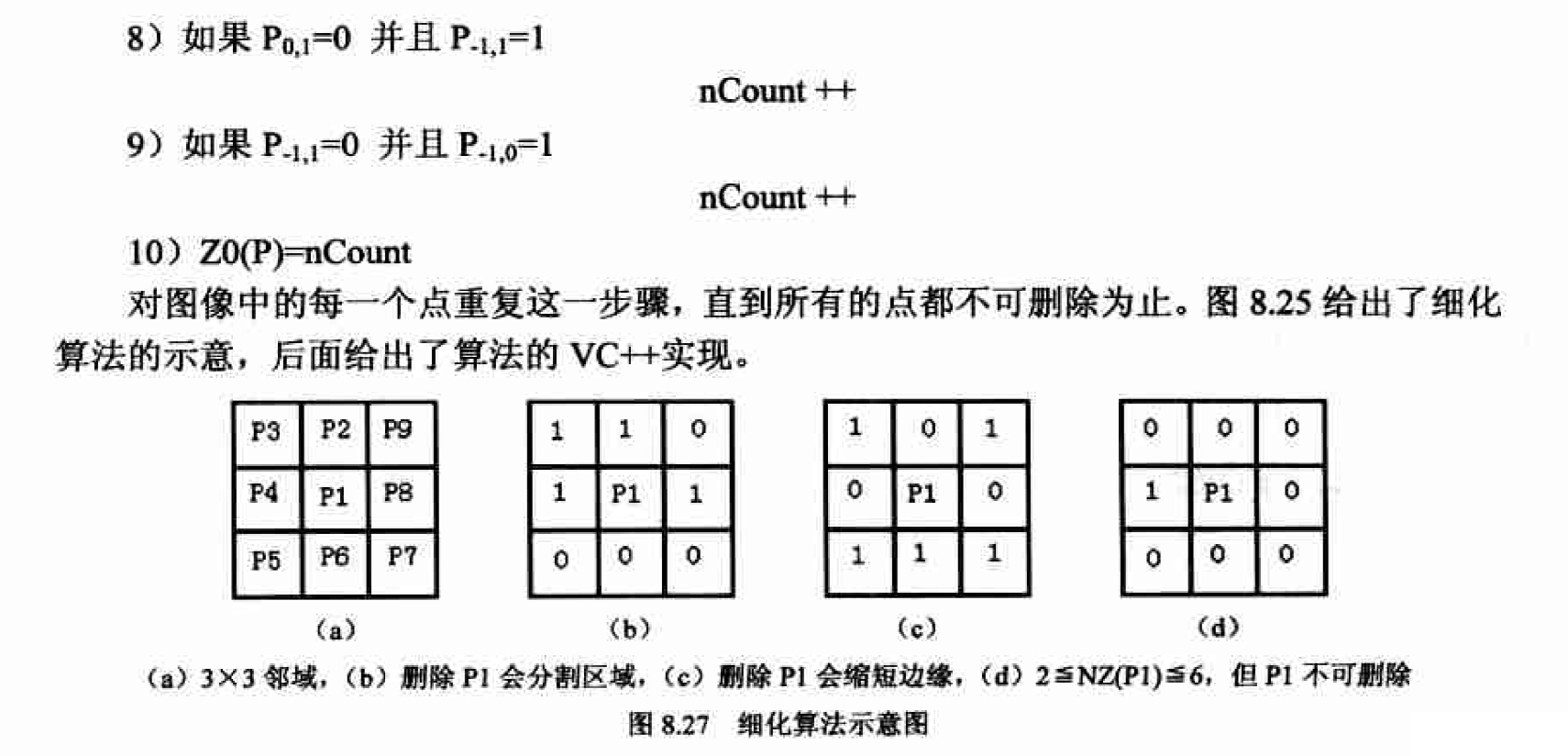
细化算法

“骨架”是指一副图像的骨髓部分，它描述物体的几何形状和拓扑结构，是重要的图像描绘子之一，计算骨架的过程一般称为“细化”或“骨架化”，在包括文字识别、工业零件形状识别以及印刷电路板自动检测在内的很多应用中，细化过程都发挥着关键作用。通常，对我们感兴趣的目标物体进行细化有助于突出目标的形状特点和拓扑结构并且减少冗余的信息量。

像素化算法

细化适用于和物体拓扑结构或形状有关的应用， 如前述的手写字符识别。 但有时我们关心的是目标对象是否存在、 它们的位置关系， 或者个数， 这时在预处理中加入像素化步骤会给后续的图像分析带来极大的方便

理论基础
像素化操作首先需找到二值图像中所有的连通区域， 然后用这些区域的质心作为这些连通区域的代表， 即将1个连通区域像素化为位于区域质心位置的1个像素。
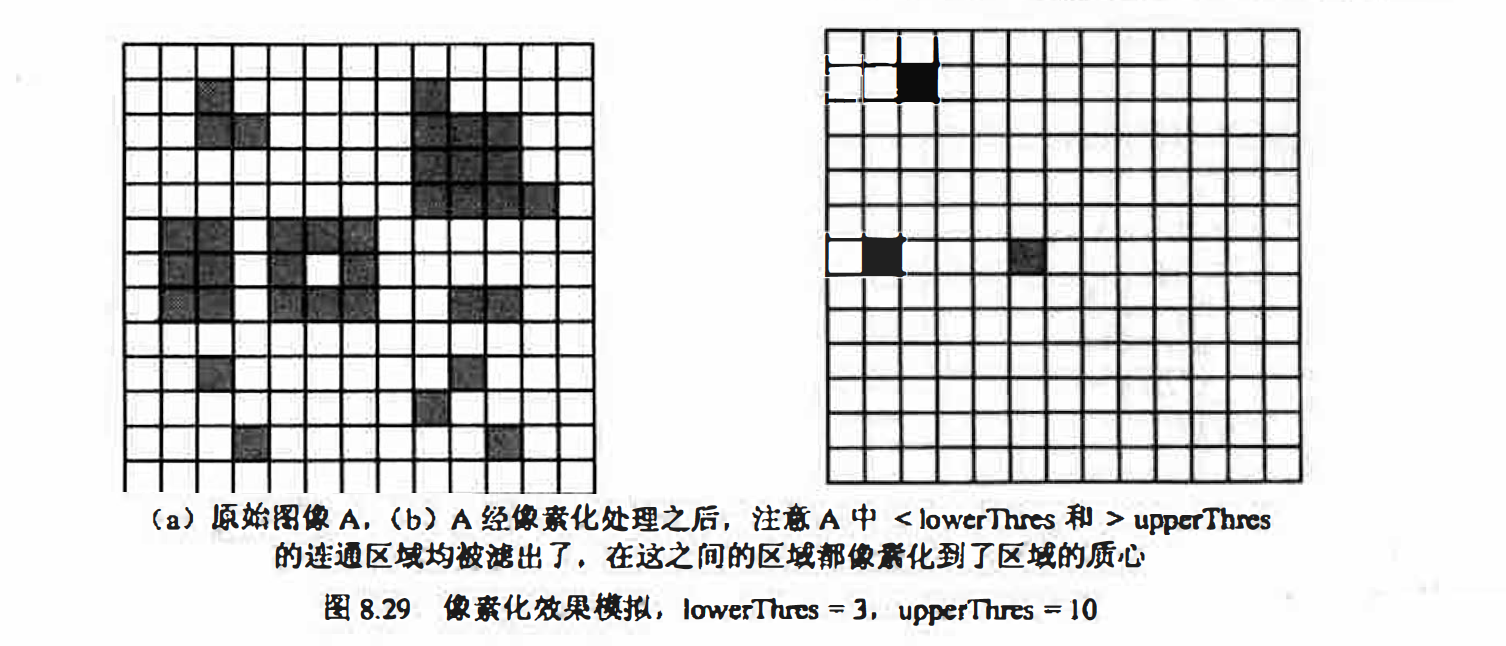
有时还可以进一步引入一个低阀值lowerThres和一个高阙值highThres来指出图像中我们感兴趣的对象连通数(连通分量中的像素数目)的大致范围， 从而只像素化图像中大小介于lowerThres和upperThres之间的连通区域， 而连通数低于lowerThres或高于upperThres的对象都将被滤除， 这就相当于使用算法的同时具有了过滤噪声的能力。如图8.29 所示。

凸壳

如果连接物体A内任意两点的直线段都在淫的内部，则称d是凸的。任意物体A的凸亮H是包含A的最小凸物体。
我们总是希望像素化算法能够找到物体的质心来代表读物体，但在实际中，可能由于光照不均等原因导致图像在二值化后，物体本身形状发生缺损，像素化算法就无法找到物体真正的质心。此时可适当地进行凸壳处理，弥补凹损，算法会找到包含原始形状的最小凸多边形，如下图8.30所示．
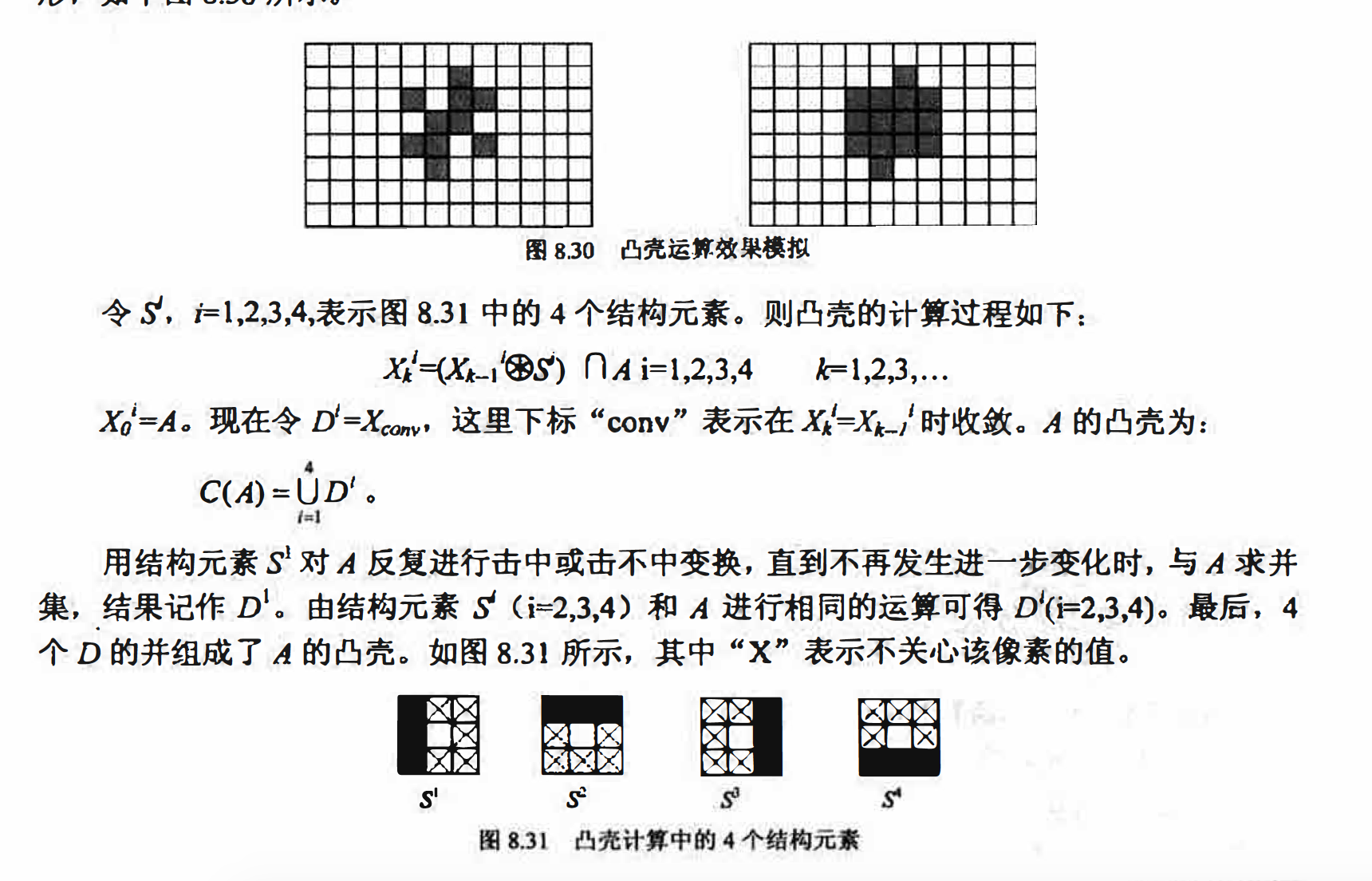为确保在上述生长过程中凸壳不会大幅超出凸性所需的最小尺寸， 可以限制其生长以便凸壳不会超出初始时包含物体A的最小矩形．

bwmorph函数
本章的很多形态学操作都可由IPT函数bwmorph实现， 该函数的调用语法为：
Iout = bwmorph(I,operation,n);
operation是一个指定操作类型的字符串， 常用的合法取位如在8.2 所示

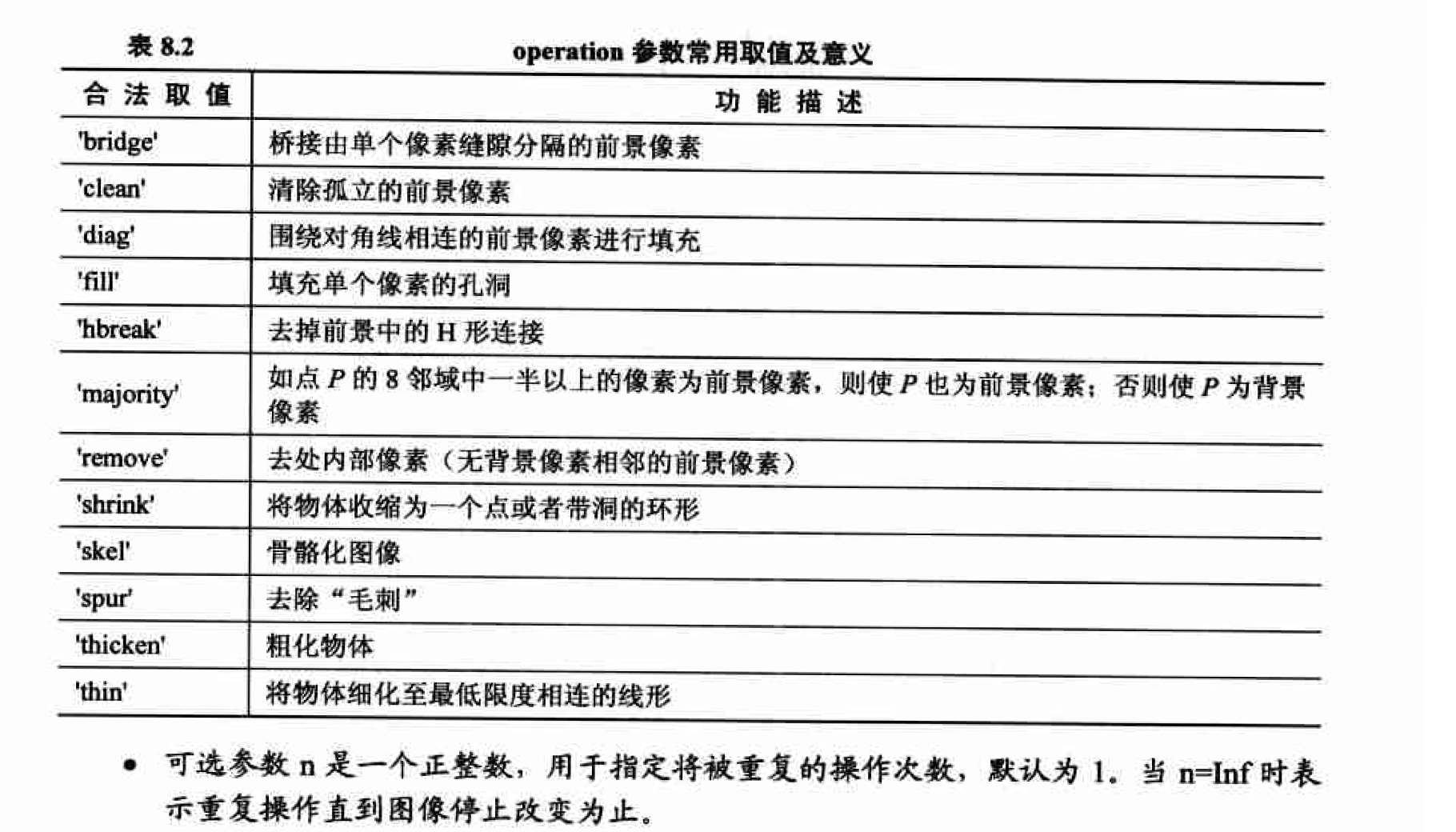
灰度图像中的基本形态学运算

本节就们把二值图像的形态学处理扩展到灰度图像的基本操作， 包括灰度膨胀、灰皮腐蚀、灰度开和灰皮闭。此外， 8.4.4 小节还将介绍一个灰度形态学的经典应用一一顶帽变换(top-hat）， 用以解决图像的光照不均问题．

灰度膨胀及其实现

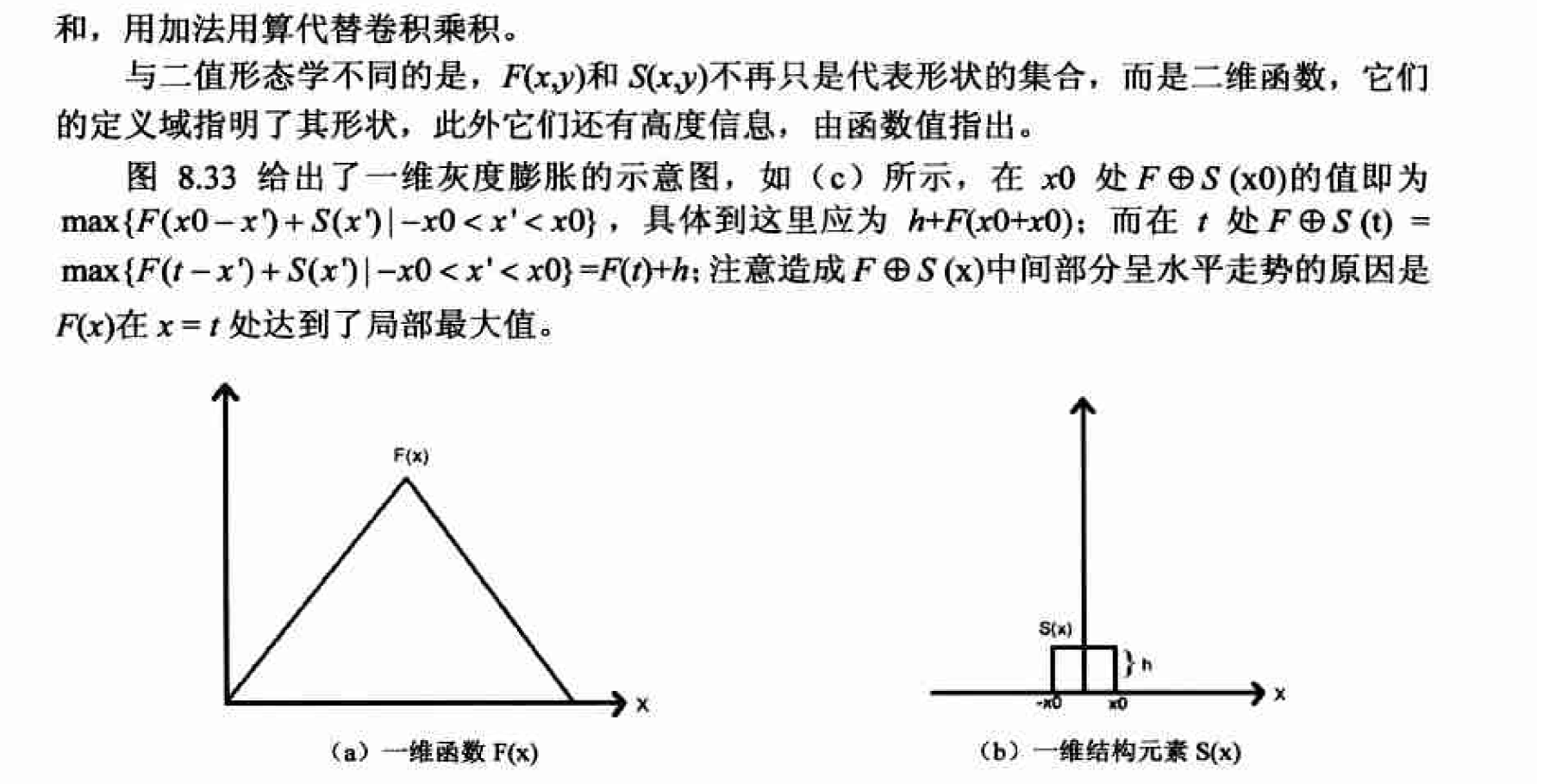
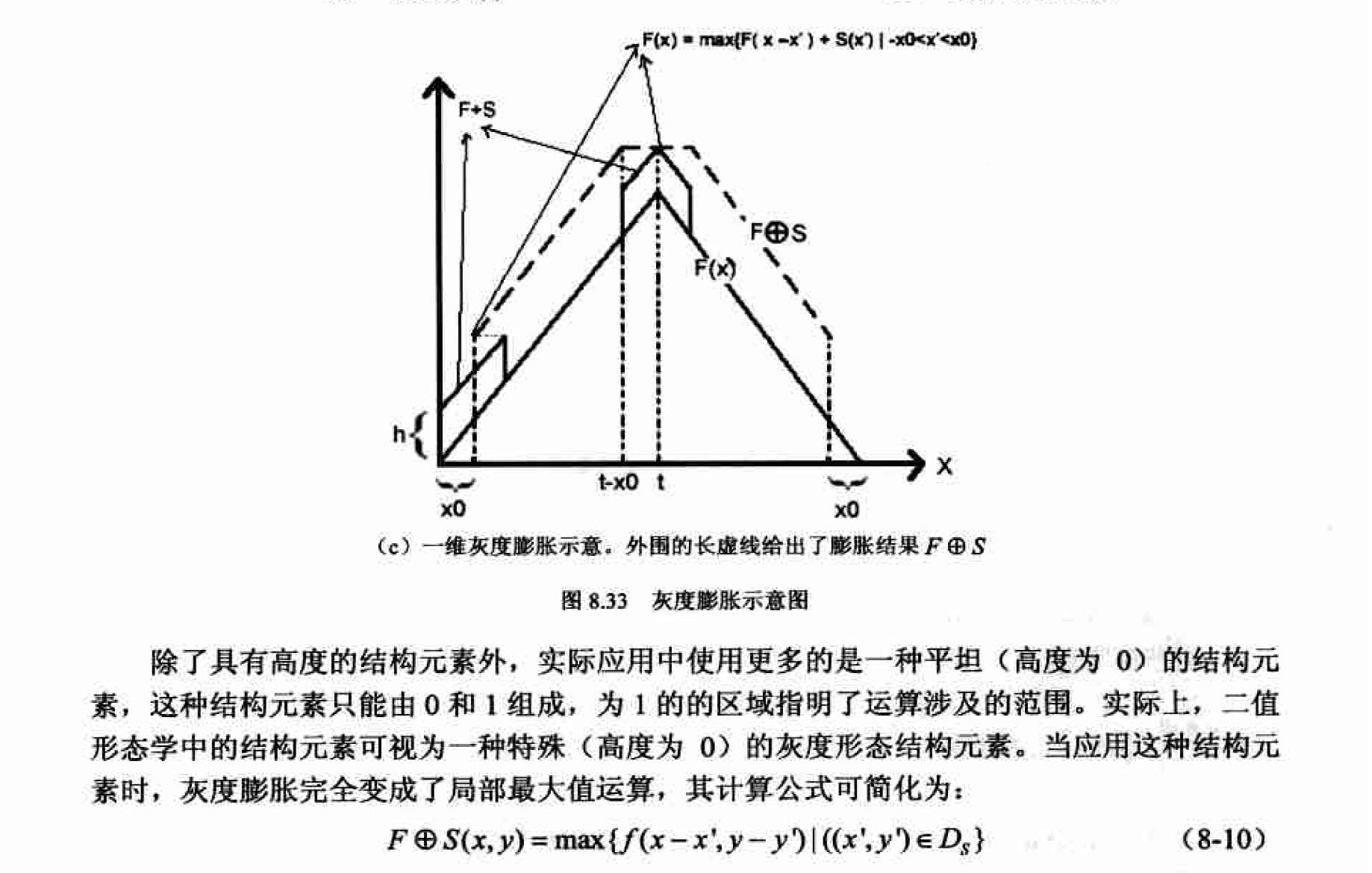
matlab实现
只要以灰度图像和相应的灰度膨胀结构元素为参数调用imdilate函数即可实现灰度膨胀，平坦结构元素的创建方法与二值形态学中相同：而非平坦结构元素也可通过 strel函数以如下方式创建。
SE = strel(NHOOD,HEIGHT);
NHOOD 为指明结构元素定义域的矩阵， 只能由0和1 组成.
HEIGHT 是一个与NHOOD 具有相同尺寸的矩阵， 指出了对应于NHOOD 中每个元素的高度．

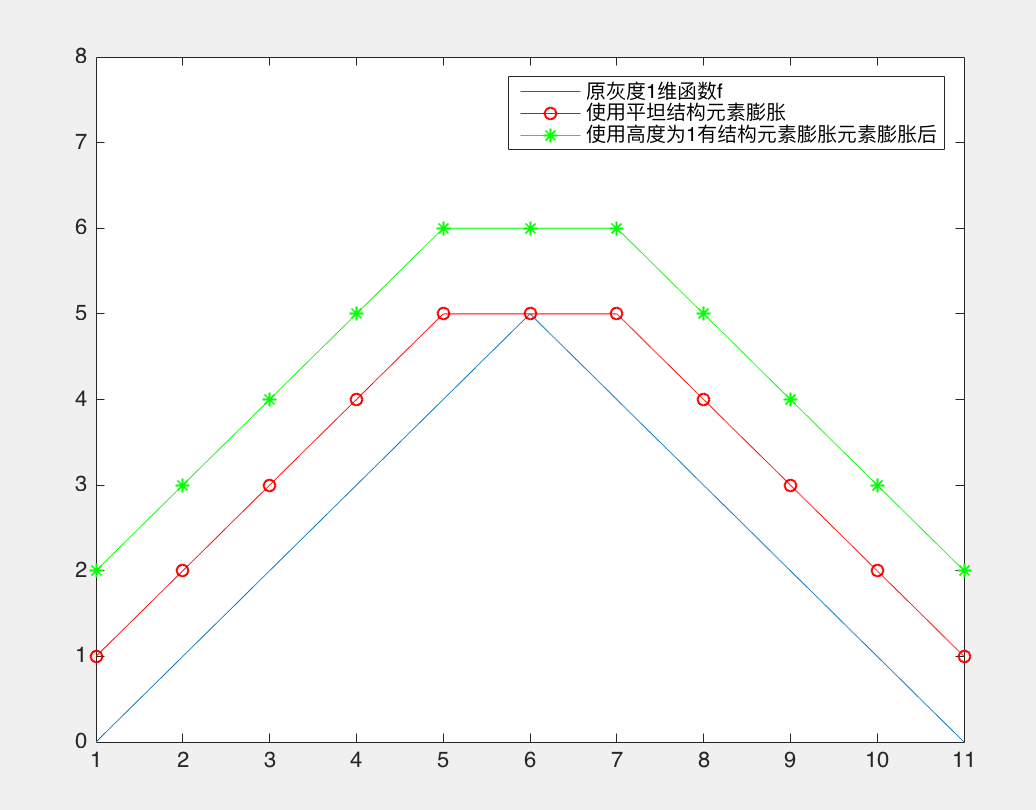
f = [0 1 2 3 4 5 4 3 2 1 0];
figure,h_f = plot(f);
seFlat = strel([1 1 1]);

fd1 = imdilate(f,seFlat);
hold on,h_fd1 = plot(fd1,'-ro');
axis([1 11 0 8]);
setHeight = strel([1 1 1],[1 1 1]);
fd2 = imdilate(f,setHeight);
hold on,h_fd2= plot(fd2,'-g*');
legend('原灰度1维函数f','使用平坦结构元素膨胀','使用高度为1有结构元素膨胀元素膨胀后');

灰度腐蚀及其实现

与二值形态学不同的是，f(x,y）和 S(x,y）不再是只代表形状的集合，而是二维函数，它们的定义域指明了其形状， 它们的值指出了高度信息。

f = [0 1 2 3 4 5 4 3 2 1 0];
figure,h_f = plot(f);
seFlat = strel([1 1 1]);

fe1 = imerode(f,seFlat);
hold on,h_fe1 = plot(fe1,'ro');
axis([1 11 0 8]);
seHeight = strel([1 1 1],[1 1 1]);

fe2 = imerode(f,seHeight);
hold on,h_fe2=plot(fe2,'-g*');
legend('原灰度1维函数f','使用平坦结构元素腐蚀','使用高度为1有结构元素膨胀元素腐蚀后');

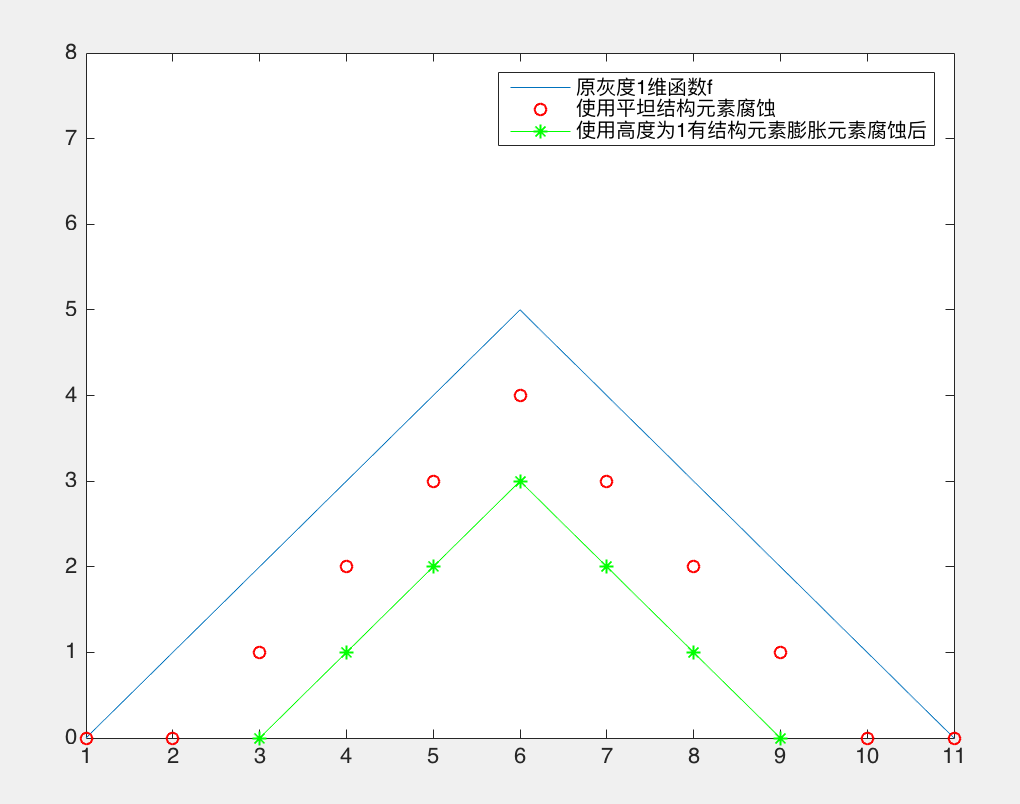
灰度膨胀和灰度腐蚀的效果比较

I = imread('lena.bmp');
seHeight=strel(ones(3,3),ones(3,3));
Idi1= imdilate(I,seHeight);
Iero = imerode(I,seHeight);
subplot(1,3,1),imshow(I);
subplot(1,3,2),imshow(Idi1);
subplot(1,3,3),imshow(Iero);

我们看到在结构元素的值均大于零的情况下， 灰度膨胀的输出图像总体上比输入图像更亮，这是局部最大值运算作用的结果。此外原图像中一些能够包含于结构元素的暗细节〈如 一部分帽子的槽皱和尾穗）被完全消除， 其余的大部分暗部细节也都得到了一定程度上的减少。而灰度腐蚀的作用正好相反， 输出图像比输入图像更暗， 如果输入图像中的亮部细节比结构元素小， 则亮度会得到削弱。

灰度开、 闭运算及其实现

与二值形态学类似，我们可以在灰度腐蚀和膨胀的基础上定义灰度开和闭运算．灰度开运算就是先灰度腐蚀后灰度膨胀，而灰度闭运算则是先灰度膨胀后灰度腐蚀，下面分别给出定义：

这一过程： （a）为图像中的一条水平像素线：（b）和（d）分别给出了球紧贴着该像素线的下侧和上侧被动的情况：而（c）和（e）则展示了滚动过程中球的最高点形成的曲线，它们分别是开、闭运算的结果。

Matlab实现
使用imopen和imdilate同样可以对灰度图像进行开、闭运算， 用法与灰度腐蚀和膨胀类似， 这里不再赘述，在实际应用中， 开操作常常用于去除那些相对于结构元素s而言较小的高灰度区域〈球体滚不上去〉，而对于较大的亮区域影响不大〈球体可以滚上去〉。虽然首先进行的灰度腐蚀 会在去除图像细节的同时使得整体灰度下降， 但随后的灰度膨胀又会增强图像的整体亮度，因此图像的整体灰度基本保持不变：而闭操作常用于去除图像中的暗细节部分， 而相对地保留高灰度部分不受影响．

顶帽交换（top-hat）及其实现

作为灰度形态学的重要应用之一， 这里学习一种非均匀光照问题的解决方案一一顶帽变换技术（top-hat）.图像f的顶帽变换h定义为图像f与图像f的开运算之差， 可表示为:
h = f -(f*s)

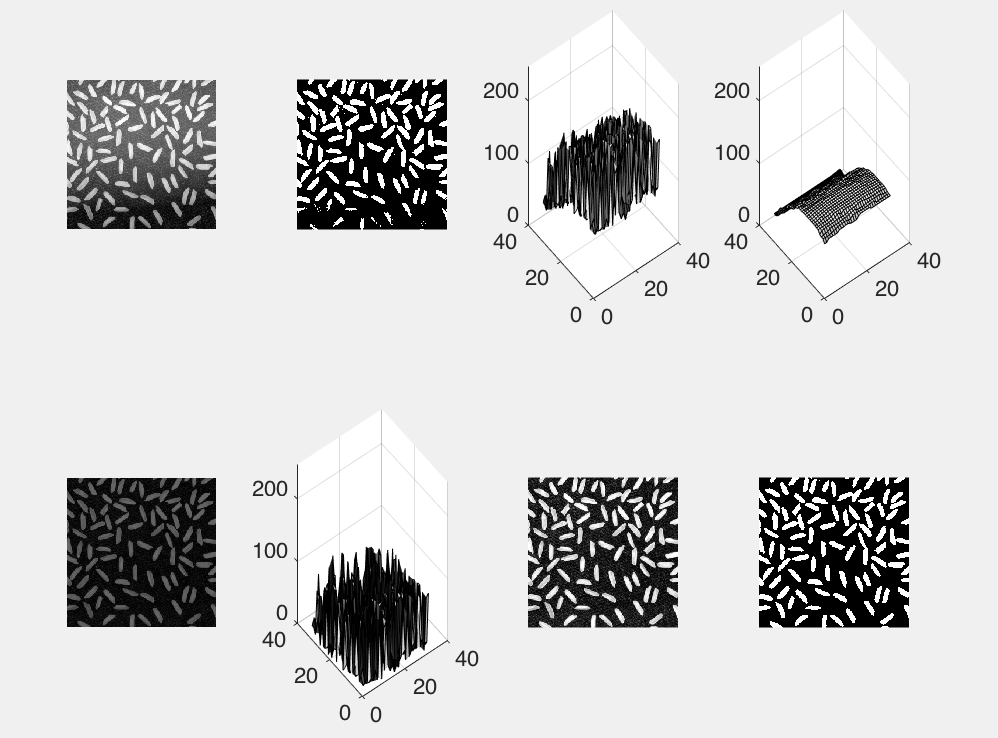
I = imread('rice.png');
subplot(2,4,1),imshow(I,[]);
thresh = graythresh(I);
Ibw = im2bw(I,thresh);
subplot(2,4,2),imshow(Ibw,[]);
subplot(2,4,3),surf(double(I(1:8:end,1:8:end))),zlim([0 255]),colormap;

bg = imopen(I,strel('disk',15));
subplot(2,4,4),surf(double(bg(1:8:end,1:8:end))),zlim([0 255]),colormap;

Itophat = imsubtract(I,bg);
subplot(2,4,5),imshow(Itophat);
subplot(2,4,6),surf(double(Itophat(1:8:end,1:8:end))),zlim([0 255]);

I2 = imadjust(Itophat);
subplot(2,4,7),imshow(I2);
thresh2 = graythresh(I2);
Ibw2 = im2bw(I2,thresh2);
subplot(2,4,8),imshow(Ibw2);

• ← Previous Post
• Next Post →