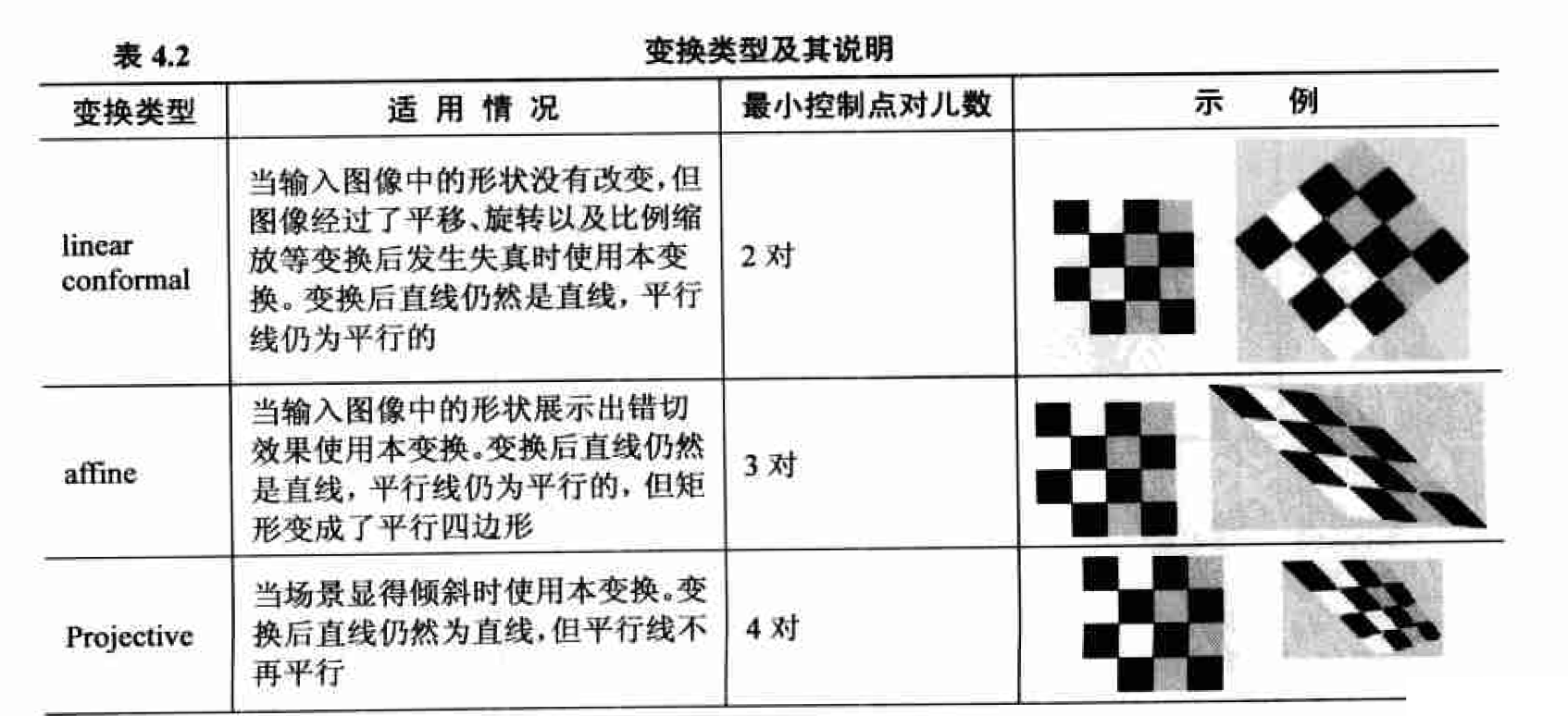
包含相同内容的两幅图像可能由于成像角度、透视关系乃至镜头自身原因所造成的几何失 真而呈现出截然不同的外观,这就给观测者或是图像识别程序带来了困扰。通过适当的几何变 换可以最大程度地消除这些几何失真所产生的负面影响,有利于我们在后续的处理和识别工作 中将注意力集中子图像内容本身,更确切地说是图像中的对象,而不是该对象的角度和位置等。 因此, 几何变换常常作为其他图像处理应用的预处理步骤, 是图像归一化的核心工作之一。
本文主要包括以下内容
- 图像的各种几何变换, 如平移、镜像和旋转等
- 插值算法
- 图像配准
- 本章的典型案例分析
- 基于直方图均衡化的图像灰度归一化
- 汽车牌照的投影失真校正
解决几何变换的一般思路
图像几何变换又称为图像空间变换, 它将一幅图像中的坐标位置映射到另一幅图像中的
新坐标位置. 我们学习几何变换的关键就是要确定这种空间映射关系, 以及映射过程中的变
换参数。
几何变换不改变图像的像素值, 只是在图像平面上进行像素的重新安排。一个几何变换
需要两部分运算:首先是空问变换所需的运算, 如平移、旋转和镜像等, 需要用它来表示输
出图像与输入图像之间的〈像素〉映射关系:此外, 还需要使用灰度插值算法, 因为按照这
种变换关系进行计算, 输出图像的像素可能被映射到输入图像的非整数坐标上。


之所以要逆变换是因为:

图像平移
图像平移就是将图像中所有的点按照指定的平移量水平或者垂直移动。
图像平移的变换公式

对于原图中被移出图像显示区域的点通常也有两种处理方法:直接丢弃或者通过加目标图像的尺寸〈将新生成的图像宽度增加$T_x$,高度增加$T_y$〉的方法使新图像中能够包含这些点,在稍后给出的程序实现中,我们来用了第一种处理方法。.
init = imread('lena.bmp'); % 读取图像
[R, C] = size(init); % 获取图像大小
res = zeros(R, C); % 构造结果矩阵。每个像素点默认初始化为0(黑色)
delX = 50; % 平移量X
delY = 50; % 平移量Y
tras = [1 0 delX; 0 1 delY; 0 0 1]; % 平移的变换矩阵
for i = 1 : R
for j = 1 : C
temp = [i; j; 1];
temp = tras * temp; % 矩阵乘法
x = temp(1, 1);
y = temp(2, 1);
% 变换后的位置判断是否越界
if (x <= R) & (y <= C) & (x >= 1) & (y >= 1)
res(x, y) = init(i, j);
end
end
end;
figure;
subplot(1,2,1);
imshow(uint8(init)); title('原图像');
subplot(1,2,2);
imshow(uint8(res)); % 显示图像
title('平移后');

图像镜像
镜像变换又分为水平镜像和坚直镜像。水平镜像即将图像左半部分和右半部分以图像坚直中轴线为中心轴进行对换;而竖直镜像则是将图像上半部分和下半部分以图像水平中轴线为中心轴进行对换.
图像镜像的交换公式

matlab实现
imtransform函数用于完成一般的二维空间变换,形式如下:
B=imtransform(A,TFrom,method)
A=imread('lena.bmp');
[height,width,dim]=size(A);
tform= maketform('affine',[-1 0 0;0 1 0;width 0 1]);
B = imtransform(A,tform,'nearest');
tform2=maketform('affine',[1 0 0;0 -1 0;0 height 1]);
C = imtransform(A,tform2,'nearest');
subplot(1,3,1),imshow(A);
title('原图像');
subplot(1,3,2),imshow(B);
title('水平镜像');
subplot(1,3,3),imshow(C);
title('竖直镜像');

图像转置
图像转置是指将图像像素的x坐标和y坐标互换,图像的大小会随之改变:高度和宽度将互换。
图像转置的交换公式

matlab实现
A = imread('lena.bmp');
tform = maketform('affine',[0 1 0;1 0 0;0 0 1]);
B = imtransform(A,tform,'nearest');
subplot(1,2,1),imshow(A);
title('原图像');
subplot(1,2,2),imshow(B);
title('图像转置');

图像缩放
图像缩放是指图像大小按照指定的比率放大或者缩小
图像缩放的变换公式

直接根据缩放公式计算得到的目标图像中,某些映射源坐标可能不是整数,从而找不到
对应的像素位置。例如,当$S_x=S_y=2$ 时,图像放大2倍,放大图像中的像素(0, 1)对应于
原图中的像素(0, 0.5),这不是整数坐标位置,自然也就无法提取其灰度值。因此我们必须
进行某种近似处理,这里介绍一种简单的策略即直接将它最邻近的整数坐标位置(0,0)或者
(0,1)处的像素灰度值赋给它,这就是所谓的最近邻插值。当然还可以通过4.7节将介绍的其
他插值算法来近似处理.
matlab实现
缩放变换仍然可借助前面几节中使用的imtransform函数来实现。此外,Matlab还提供
专门的图像缩放函数imresize,具体调用形式为:
B = imresize(A,Scale,method);
参数说明:
a为缩放的原始图像
Scale为统一缩放比例
method用于指定插值方法,其合法取值同imtransform
A = imread('lena.bmp');
B = imresize(A,1.2,'nearest');
figure,imshow(A);title('原图像');
figure,imshow(B);title('图像缩放');
图像旋转
旋转一般是指将图像围绕某一指定点旋转一定的角度。旋转通常也会改变图像的大小, 和4.2 节中图像平移的处理一样, 可以把转出显示区域的图像截去, 也可以改变输出图像的 大小以扩展显示范围.
以原点为中心的图像旋转
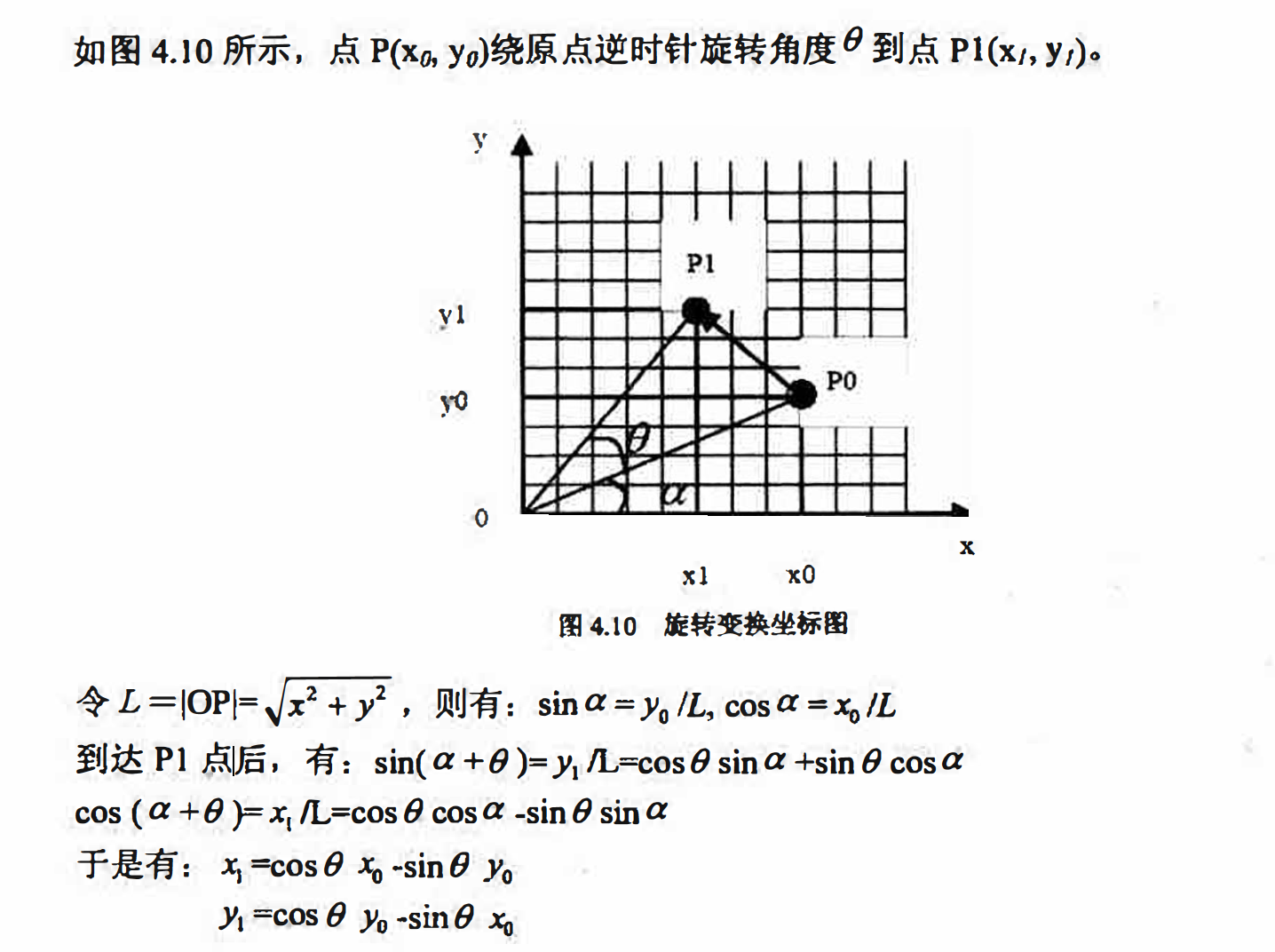
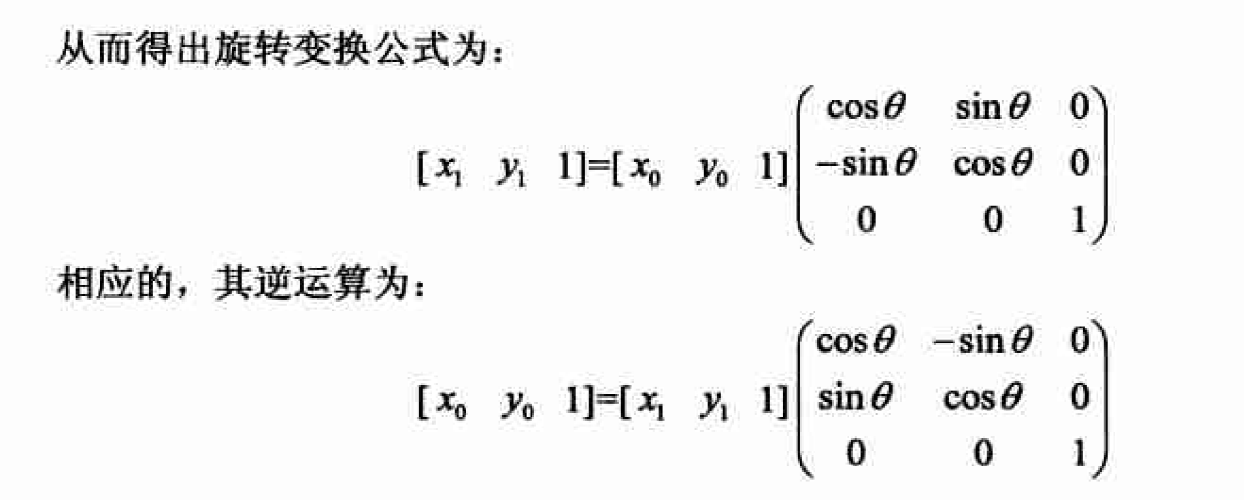
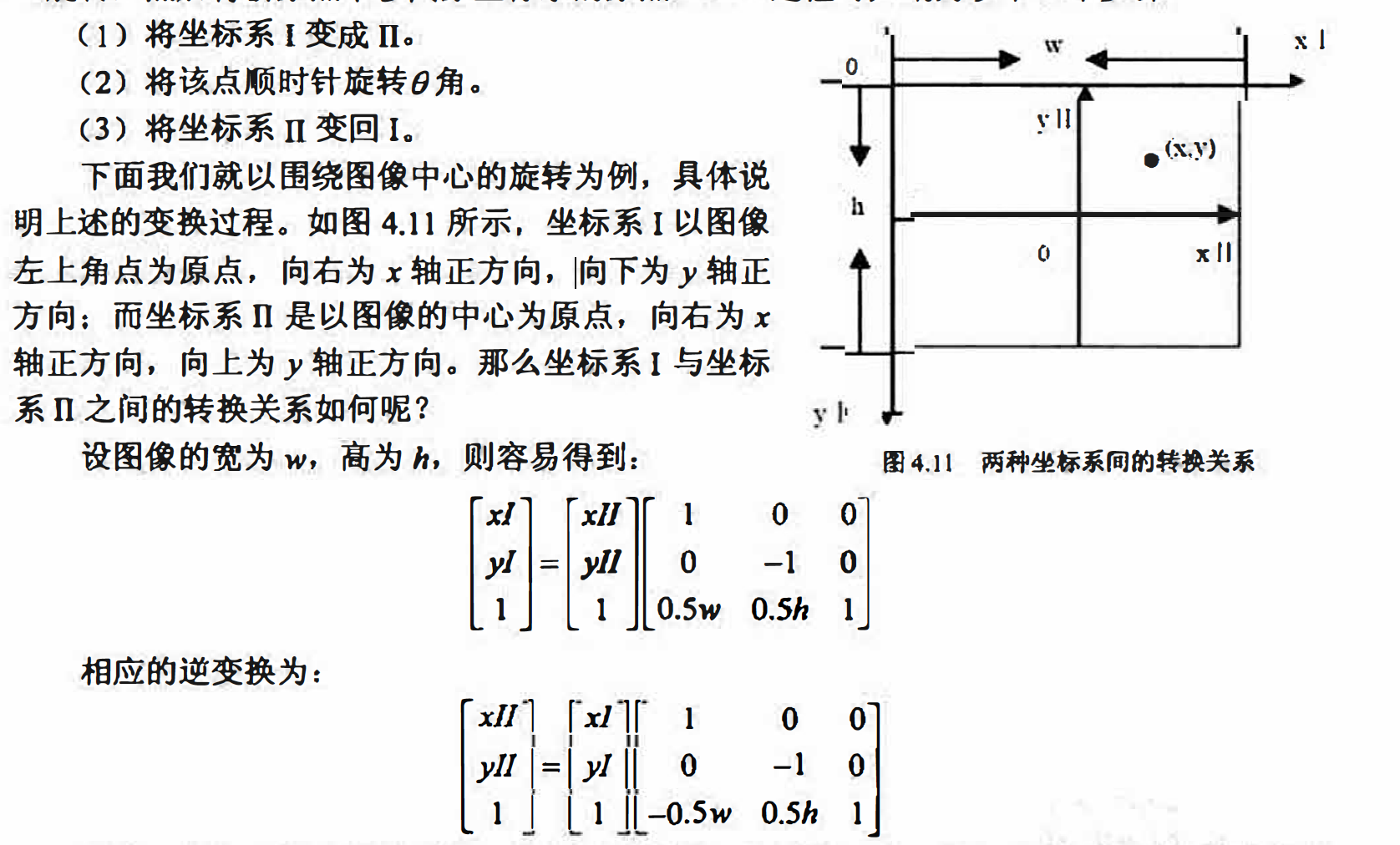
以任意点为中心的图像旋转
在4.6.1小节中给出的旋转示例是以坐标原点为中心进行的,那么如何围绕任意的指定
点来旋转呢?将平移和旋转操作相结合即可,即先进行坐标系平移,再以新的坐标原点为中
心旋转,然后将新原点平移回原坐标系的原点。这一过程可归纳为以下3个步骤:
至此,我们已经实现了上述3个步骤中的第1步和第3步,再加上第2步的旋转变换就
得到了围绕图像中心点旋转的最终变换矩阵,该矩阵实际上是3个变换步骤中分别用到的3
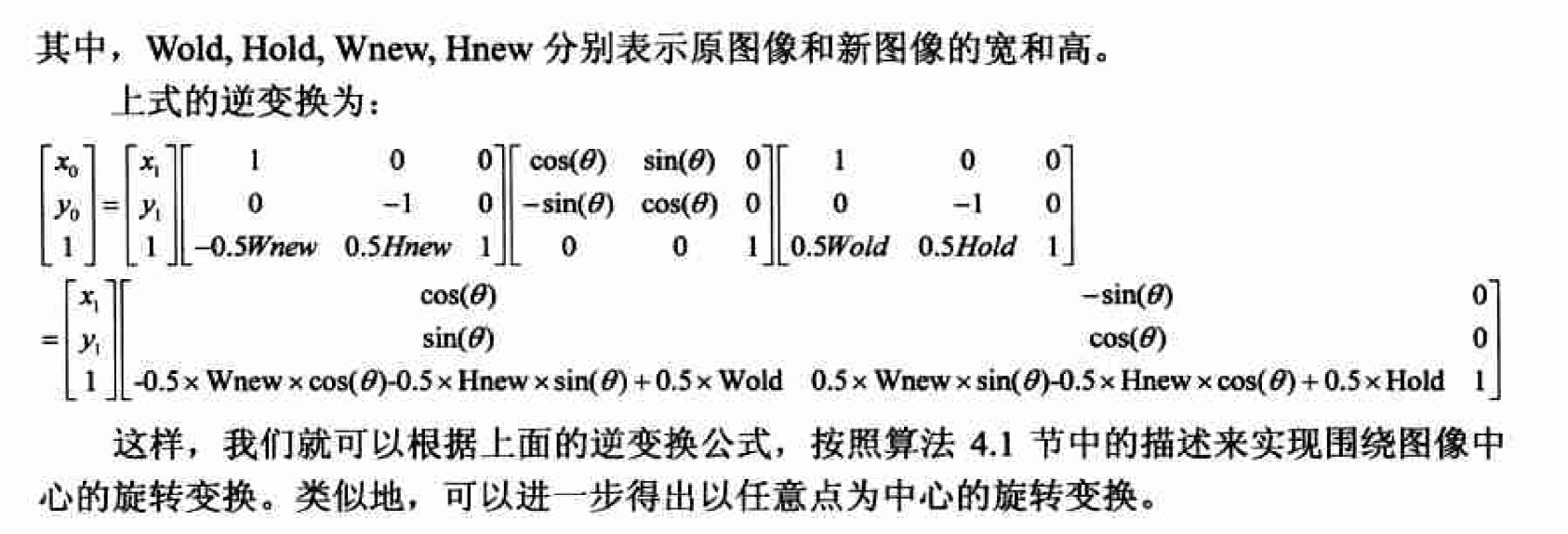
个变换矩阵的级联。
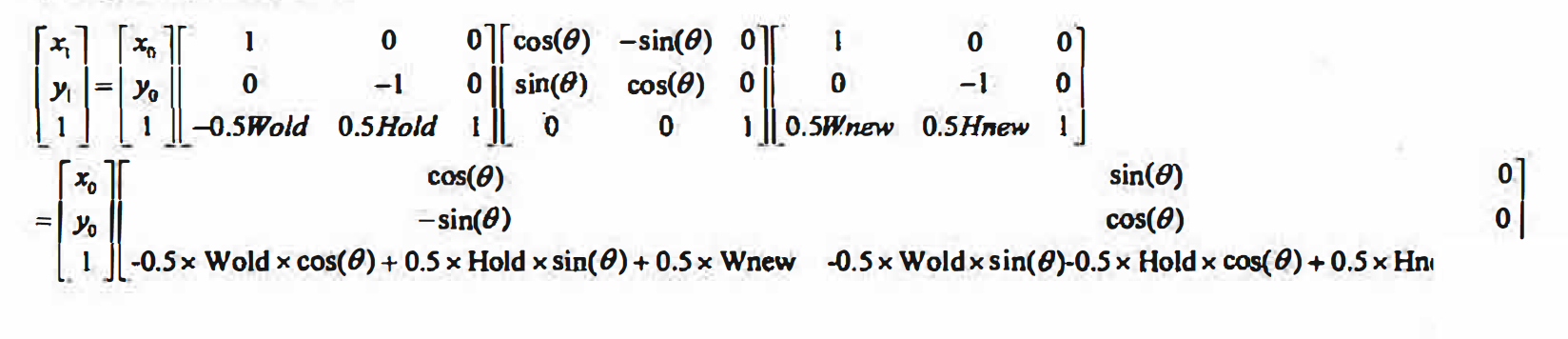
matlab实现
图像旋转变换的效果受具体插值方法的影响较为明显,本节给出的实现均采用最近邻插 值,在 4.7 节中将给出来用不同的插值算法时图像旋转变换的效果比较。
可通过4.6.2 小节中学习的方法设置适当的变换结构TFORM,从而调用imtansform来
实现以任意点为中心的图像旋转。此外, Matlab 还专门提供了围绕图像中心的旋转变换函数
imrotate ,其调用方式如下:
B=imrotate(A,angle,method,’crop’)
参数说明:
- A是要旋转的图像.
• angle 为旋转角度,单位为度,如果为其指定一个正值,则imrotate 函数接逆时针方 向旋转圈像. · 可选参数method为imrotate 函数指定插佳方法. • ‘crop'选项会裁剪旋转后增大的图像,使得到的圈像和原图大小一致.
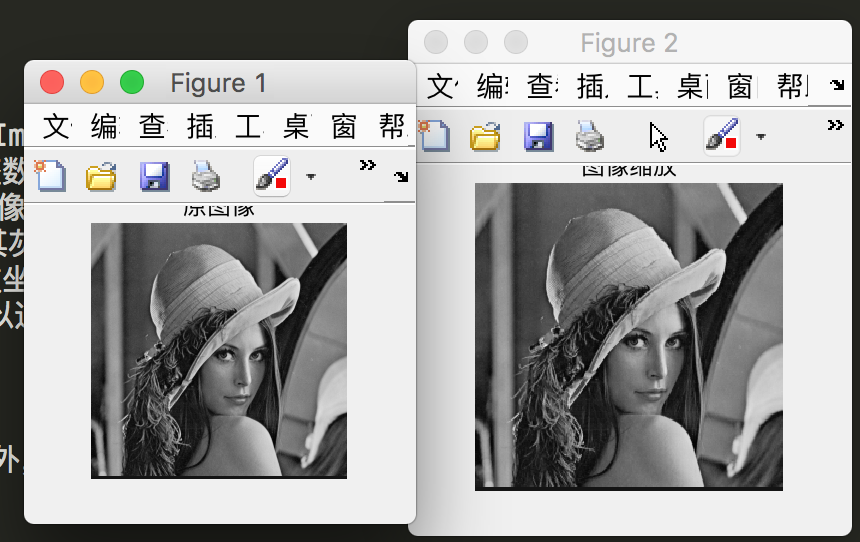
A = imread('lena.bmp');
B = imrotate(A,30,'nearest','crop');
subplot(1,2,1),imshow(A);
title('原图像');
subplot(1,2,2),imshow(B);
title('逆时针旋转30度');

插值算法
实现几何运算时, 有两种方法。第一种称为向前映射法, 其原理是将输入图像的灰度逐 个像索地转移到输出图像中,即从原图像坐标计算出目标图像坐标: $g(x_1,y_1) = f(a(x_o,y_o}, b(x_o, y_o))$。前面的平移、镜像等操作就可以采用这种方法。
另外一种称为向后映射法, 它是向前映射变换的逆操作, 即输出像素逐个映射回输入图 像中。如果一个输出像素映射到的不是输入图像来样栅格的整数坐标处的像素点, 则其灰度 值就需要基于整数坐标的灰度值进行推断, 这就是插值。由于向后映射法是逐个像素产生输 出图像, 不会产生计算浪费问题, 所以在缩放、旋转等操作中多采用这种方法, 本书采用的 也全部为向后映射法。
最近邻插值
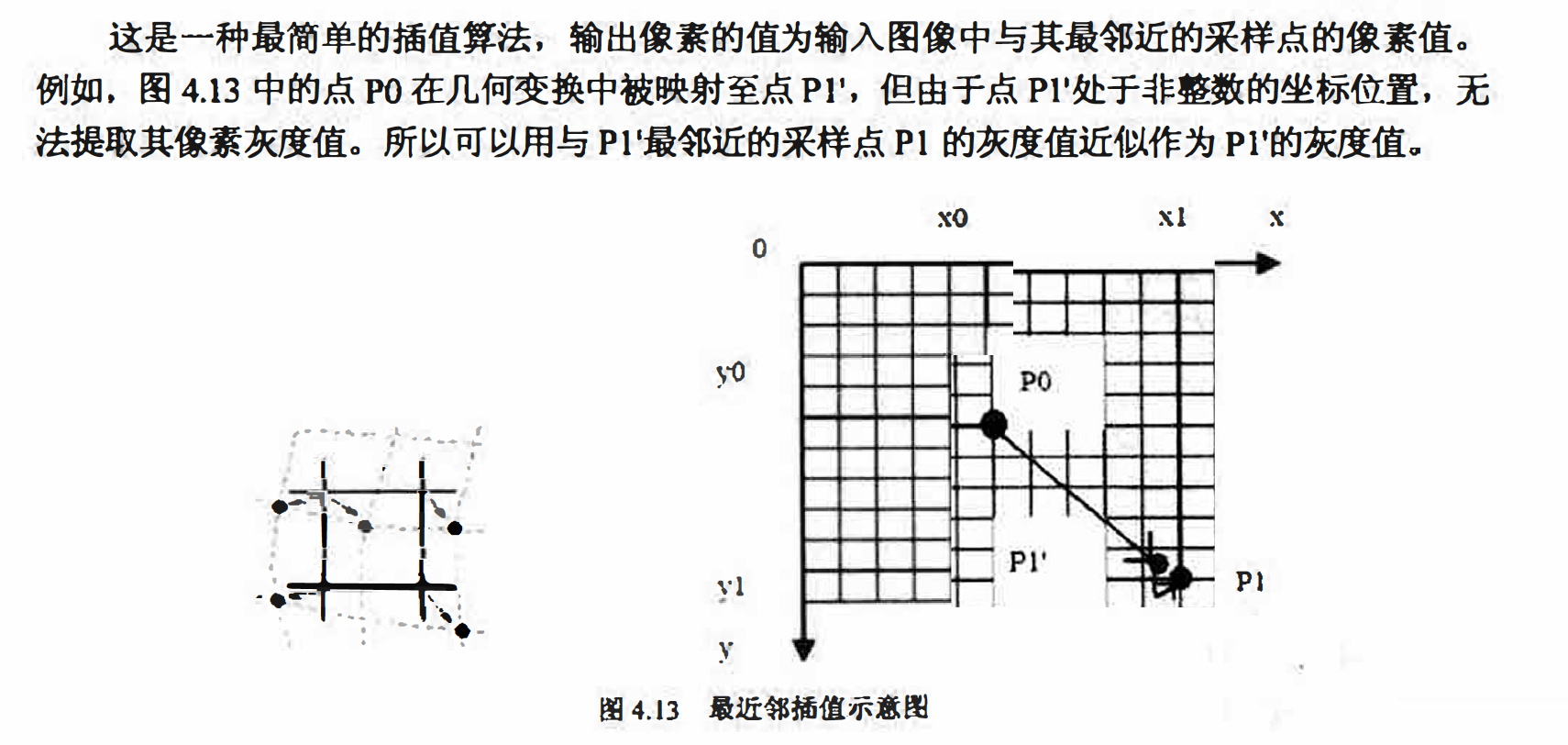
最近邻插值可表示为:
f(x,y) = g(round(x), round (y) );
我们在之前的各种变换Visual C++实现中均采用了最近邻插值的算法,因为它计算简单,
而且在很多情况下的输出效果也可以接受。然而, 最近邻插值法会在图像中产生人为加工的
痕迹, 详见例4.1.
双线性插值
双线性插值又称为一阶插值,是线性插值扩展到二维的一种应用。它可以通过一系列的一阶线性插值得到.
输出像素的值为输入图像中距离它最近的2×2邻域内来样点像素灰度值的加权平均。
设己知单位正方形的顶点坐标分别为f(O,0)、f(1 ,O)、f(O,1)、f(1,1), 如图4.14所示, 我们
要通过双线性插值得到正方形内任意点f(x,y)的值。
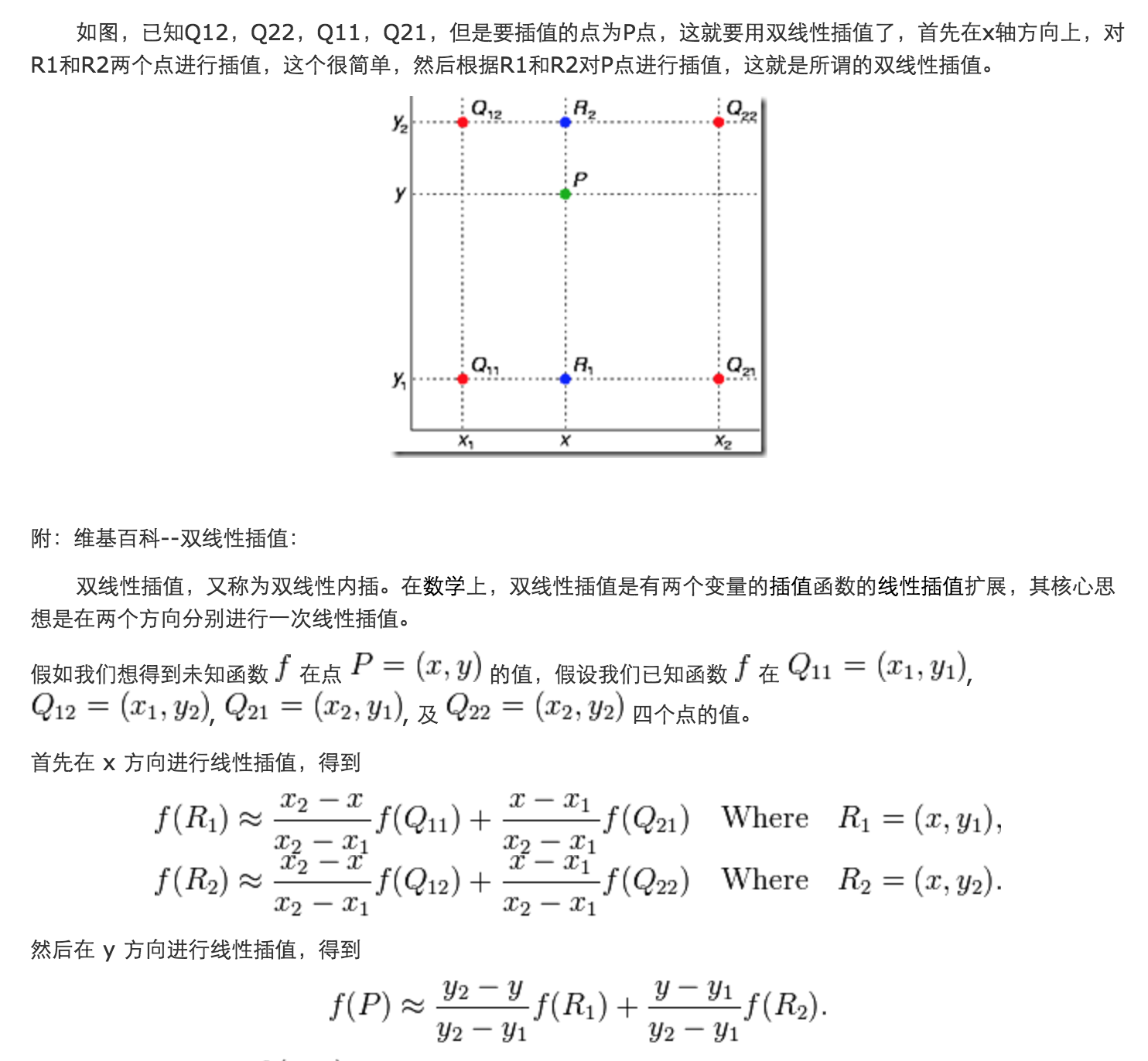
上面的推导是在单位正方形的前提下进行的, 稍加变换就可以推广到一般情况中. 线性插值的假设是原图的灰度在两个像素之问是统性变化的, 显然这是一种比较合理的 假设.因此在一般情况下,双线住插值都能取得不错的效果。更精确的方法是果用曲线插值, 即认为像素’之间的灰度变化规律符合某种曲线方程, 当然这种处理的计算量是很大的。
高阶插值
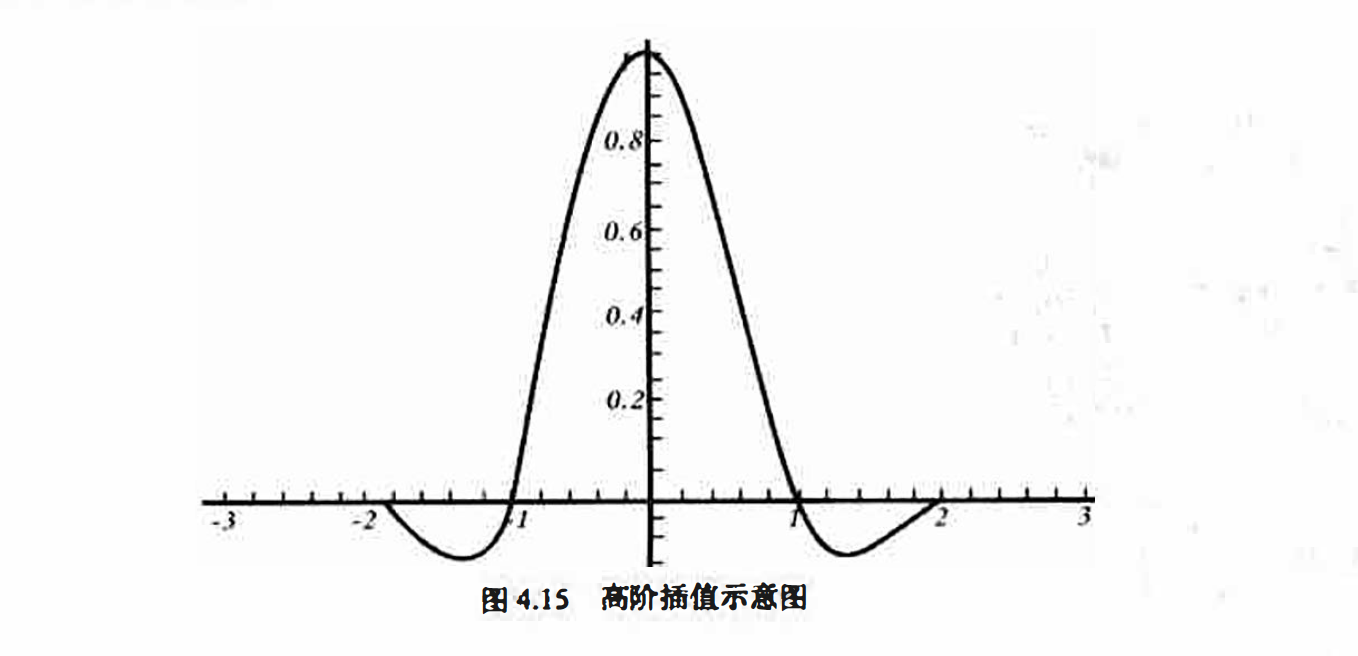
在一些几何运算中, 双线性插值的平滑作用会使图像的细节退化, 而其斜率的不连续性
则会导致变换产生不希望的结果. 这些都可以通过高阶插值得到弥补, 高阶插值常用卷积来
实现。输出像素的值为输入图像中距离它最近的4×4领域内采样点像素值的加权平均值。
下面以三次插值为例, 它使用了如下的三次多项式来逼近理论上的最佳插值函数
sin(x)/x,如图4.15 所示.

插值方法比较
下面的程序对两幅不同的图像进行图像旋转, 分别采用了最近邻、双线性和三次插值,
观察它们的不同效果.
A = imread('rectangle.bmp');
B = imrotate(A,30,'nearest');
C = imrotate(A,30,'bilinear');
D = imrotate(A,30,'bicubic');
subplot(2,2,1),imshow(A);
title('原图像');
subplot(2,2,2),imshow(B);
title('最近邻插值');
subplot(2,2,3),imshow(C);
title('双线性插值');
subplot(2,2,4),imshow(D);
title('双三次插值');

从图4.17可以看出最近邻的插值方法得到的结果还是可以接受的,但当图像中包含的像素之间灰度级有明显变化时(见图4.16),从结果图像的锯齿形边可以看出三种插值方法的效果依次递减,最近插值的效果明显不如另外两个好,锯齿比较多,而双三次插值得出的图像较好地保持了图像的细节。这是因为参与计算输出点的像章值的拟合点个数不同,个数越多效果越精确,当然参与计算的像素个数会影响计算的复杂度:实验结果也清楚地表明双三 次插值法花费的时间比另外两种的要长一些。最近邻和线性插值的速度在此次图像处理中几乎分不出来。所以,在讨算时间与质量之间有一个折中问题。
图像配准
什么是图像配准
所谓图像配准就是将同一场景的两幅或多幅图像进行对准。如航空照片的配准, 以及在
很多人脸自动分析系统中的人脸归一化, 即要使各张照片中的人脸具有近似的大小, 尽量处
于相同的位置。
一般来说, 我们以基准图像为参照, 并通过一些基准点(fudical points)找到适当的空
间变换关系s和r,对输入图像进行相应的几何变换,从而实现它与基准图像在这些基准点位
置上的对齐。
下面就以人脸图像的校准为例, 介绍如何在Matlab中实现图像配准。
Iin = imread('lena2.bmp');
Ibase = imread('lena.bmp');
figure;
subplot(1,2,1),imshow(Iin);
subplot(1,2,2),imshow(Ibase);
cpselect(Iin,Ibase);
tform = cp2tform(movingPoints,fixedPoints,'affine');