我们从一个例子开始定义推荐系统的问题。
假使我们是一个电影供应商,我们有 5 部电影和 4 个用户,我们要求用户为电影打分。
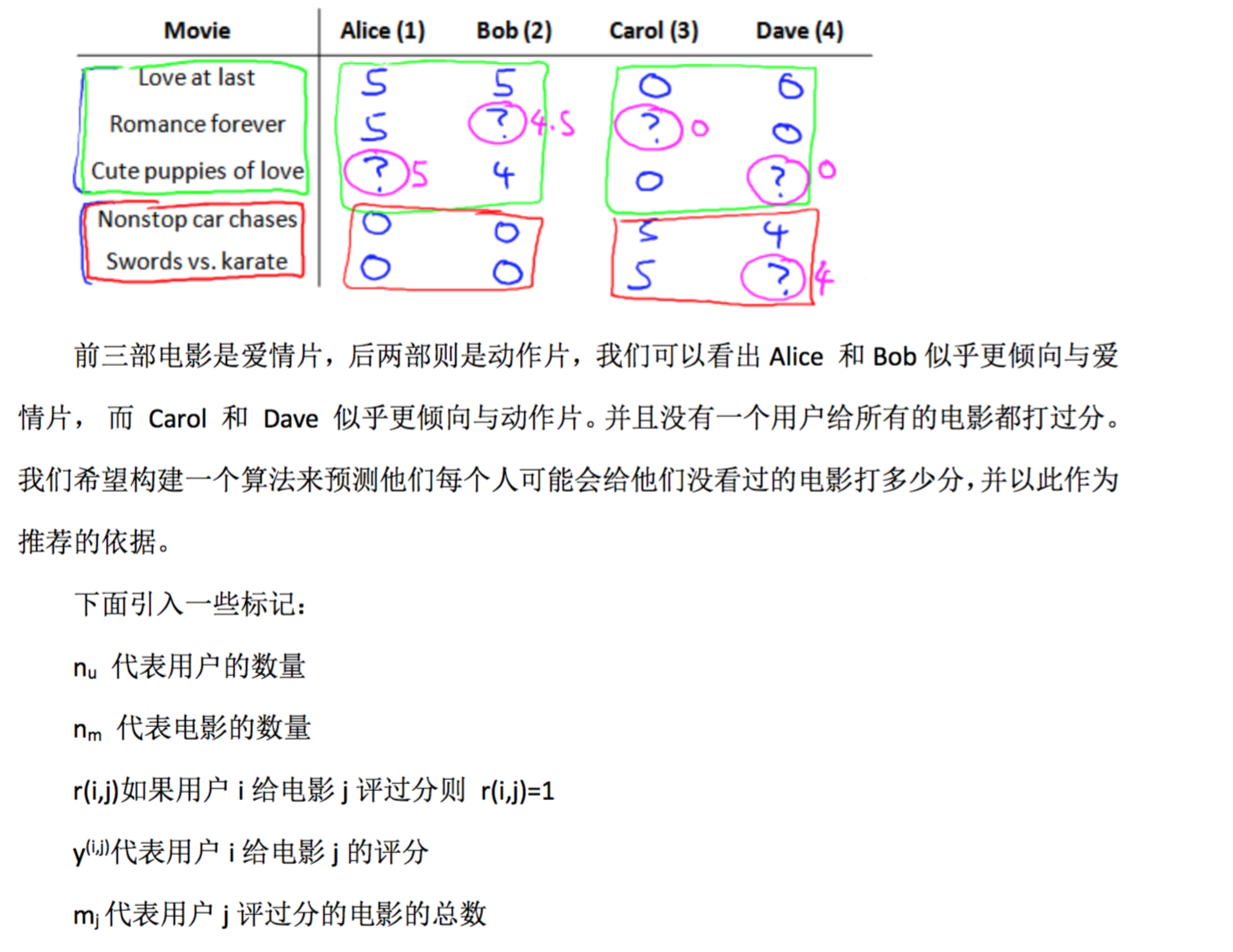
基于内容的推荐系统
在一个基于内容的推荐系统算法中,我们假设对于我们希望推荐的东西有一些数据,这 些数据是有关这些东西的特征。
在我们的例子中,我们可以假设每部电影都有两个特征,如 $x_1$ 代表电影的浪漫程度,$x_2$ 代表电影的动作程度。
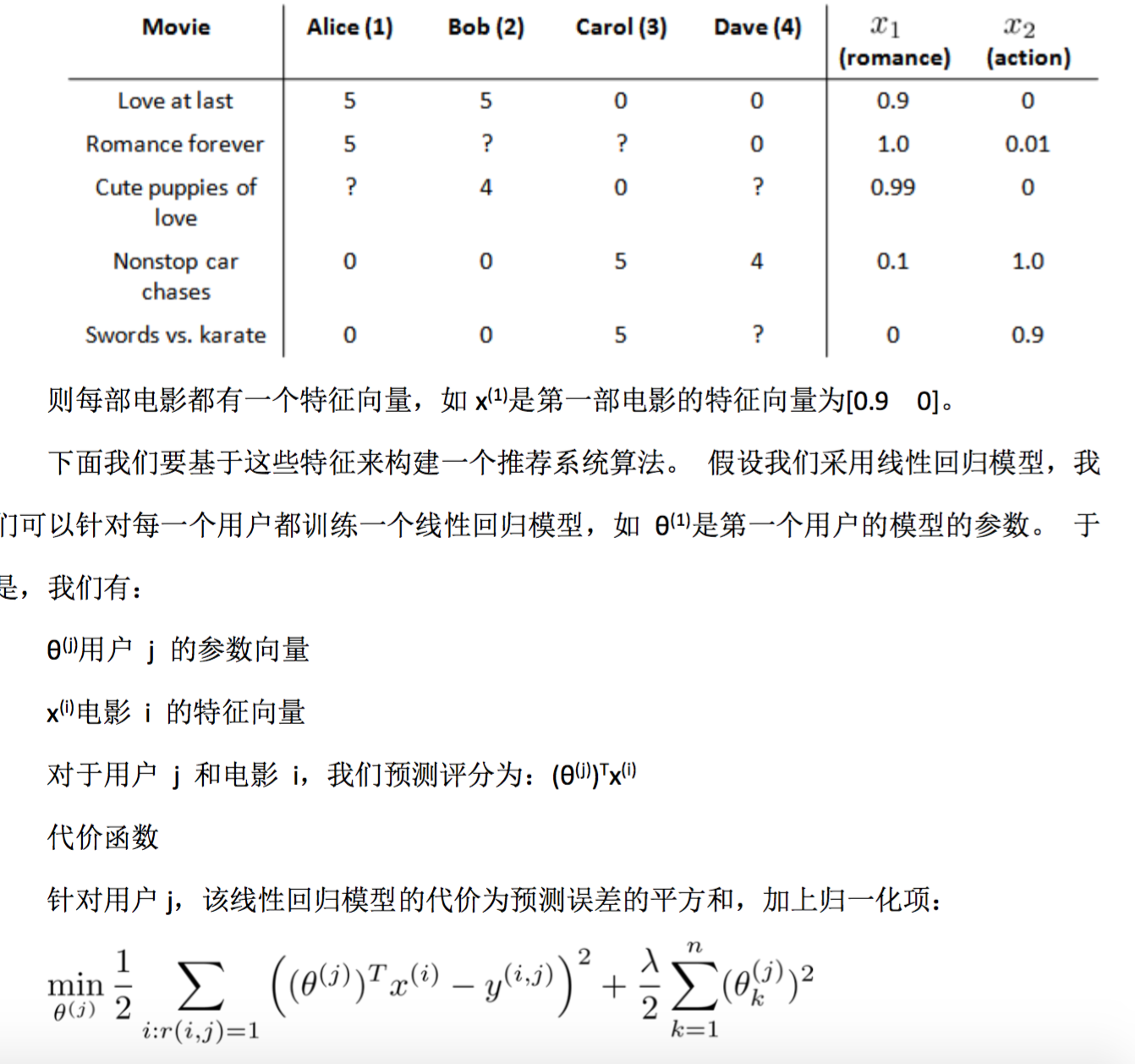
其中 i:r(i,j)表示我们只计算那些用户 j 评过分的电影。在一般的线性回归模型中,误差 项和归一项应该都是乘以1/2m,在这里我们将m去掉。并且我们不对方差项$θ_0$ 进行归一 化处理。
上面的代价函数只是针对一个用户的,为了学习所有用户,我们将所有用户的代价函数 求和:

协同过滤
在之前的基于内容的推荐系统中,对于每一部电影,我们都掌握了可用的特征,使用这 些特征训练出了每一个用户的参数。相反地,如果我们拥有用户的参数,我们可以学习得出 电影的特征。

注:在协同过滤从算法中,我们通常不使用方差项,如果需要的话,算法会自动学得。 协同过滤算法使用步骤如下:
- 初始 $x^{(1)},x^{(2)},…,x^{(nm)},θ^{(1)},θ^{(2)},…,θ^{(nu)}$为一些随机小值
- 使用梯度下降算法最小化代价函数
- 在训练完算法后,我们预测$(θ^{(j)})^Tx^{(i)}$为用户 j 给电影 i 的评分
通过这个学习过程获得的特征矩阵包含了有关电影的重要数据,这些数据不总是人能读
懂的,但是我们可以用这些数据作为给用户推荐电影的依据。 例如,如果一位用户正在观看电影 $x^{(i)}$,我们可以寻找另一部电影 $x^{(j)}$,依据两部电影的
特征向量之间的距离$||x^{(i)}-x^{(j)}||$的大小。

向量化:低秩矩阵分解
在上几节视频中,我们谈到了协同过滤算法,本节视频中我将会讲到有关该算法的向量 化实现,以及说说有关该算法你可以做的其他事情。
举例子:
1.当给出一件产品时,你能否找到与之相关的其它产品。
2.一位用户最近看上一件产品,有没有其它相关的产品,你可以推荐给他。
我将要做的是:实现一种选择的方法,写出协同过滤算法的预测情况。
我们有关于五部电影的数据集,我将要做的是,将这些用户的电影评分,进行分组并存
到一个矩阵中。
我们有五部电影,以及四位用户,那么 这个矩阵 Y 就是一个 5 行 4 列的矩阵,它将这
些电影的用户评分数据都存在矩阵里:
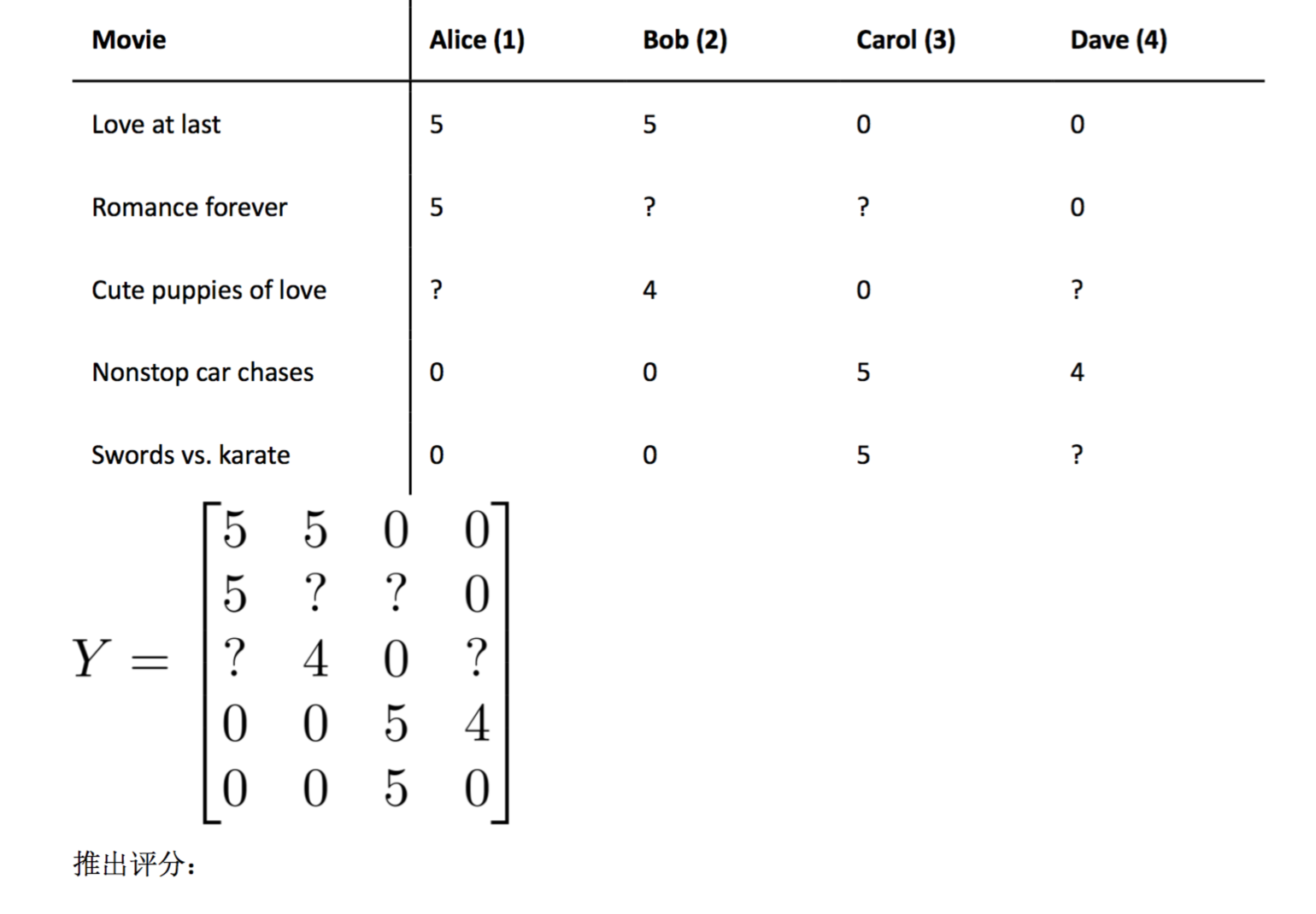

均值归一化
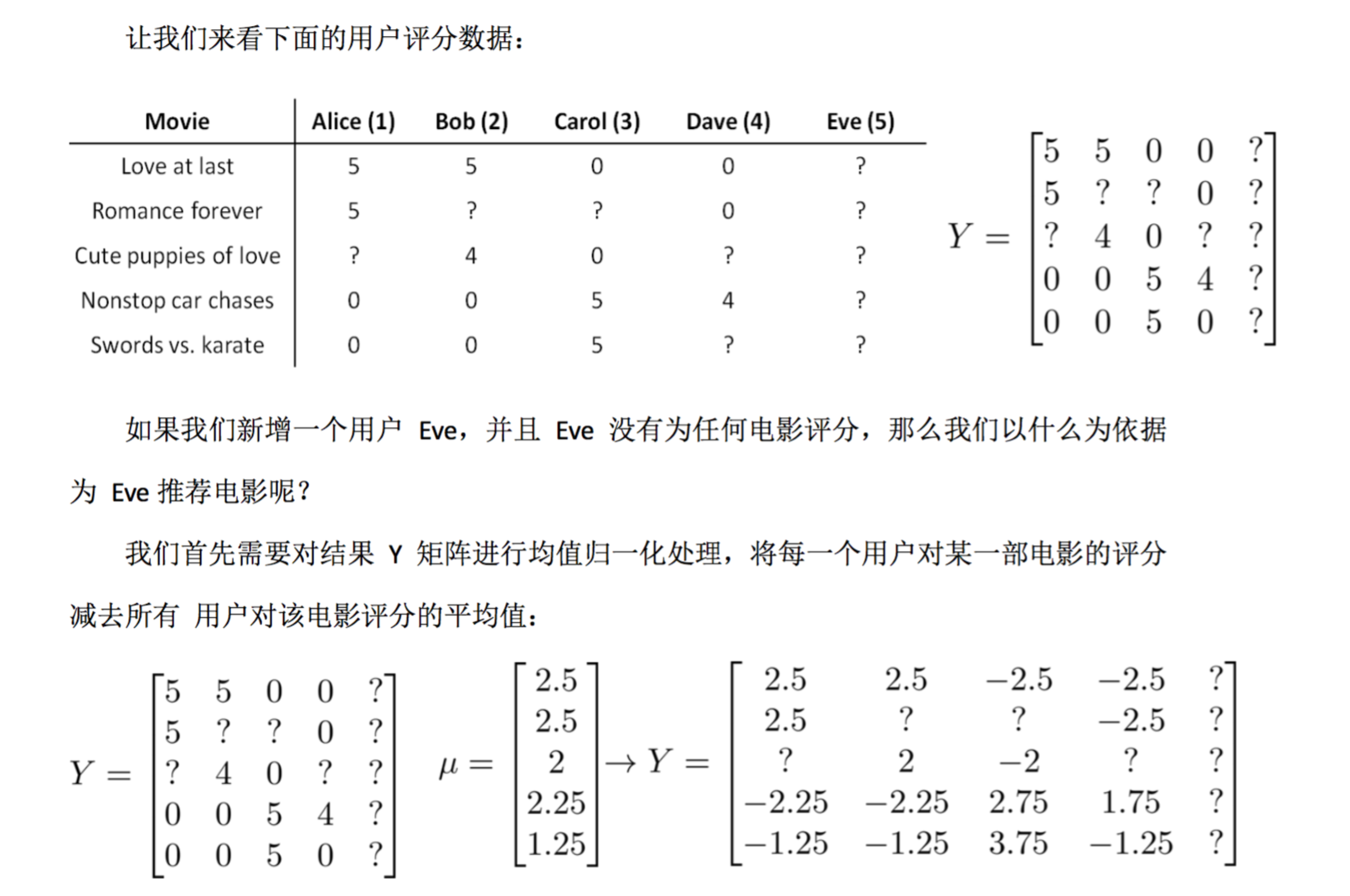
然后我们利用这个新的 Y 矩阵来训练算法。如果我们要用新训练出的算法来预测评分, 则需要将平均值重新加回去,预测$(θ^{(j)})^T(x^{(i)})+μ_i$ 对于Eve,我们的新模型会认为她给每部电影 的评分都是该电影的平均分。