1、上下标的使用
下标的输入命令为:
$_{内容}$
注意,如果内容不是单字符,一定要把下标部分放在一个{}内
下标:{x$_0$,x$_1$,x$_2$,x$_3$}
上标:{x$^0$,x$^1$,x$^2$,x$^3$}
下标:{x$_0$,x$_1$,x$_2$,x$_3$}
上标:{x$^0$,x$^1$,x$^2$,x$^3$}
2、插入分数
Latex插入分数的命令是\frac{分子}{分母}。输入如下代码:
$h_{0}(x)=\frac{1}{1+e^{-\theta}}$
更加复杂的例子
其中${x1,x2,x3}$为输入单元,x$_0$称为偏置单元(bias unit),$x_0=1$,{$x_0$,$x_1$,$x_2$,$x_3$}称为连接权重。其中$h_0(x)=\frac{1}{1+e^{-\theta^{t}*x}}$。
还记得逻辑回归的sigmoid函数吗,在这里称作“激励函数”(motivation function)$sigmoid(x)=\frac{1}{1+e^{-x}}$,其图像为(图片来自wiki):
其中${x1,x2,x3}$为输入单元,x$_0$称为偏置单元(bias unit),$x_0=1$,{$x_0$,$x_1$,$x_2$,$x_3$}称为连接权重。其中$h_0(x)=\frac{1}{1+e^{-\theta^{t}*x}}$。 还记得逻辑回归的sigmoid函数吗,在这里称作“激励函数”(motivation function)$sigmoid(x)=\frac{1}{1+e^{-x}}$,其图像为(图片来自wiki):
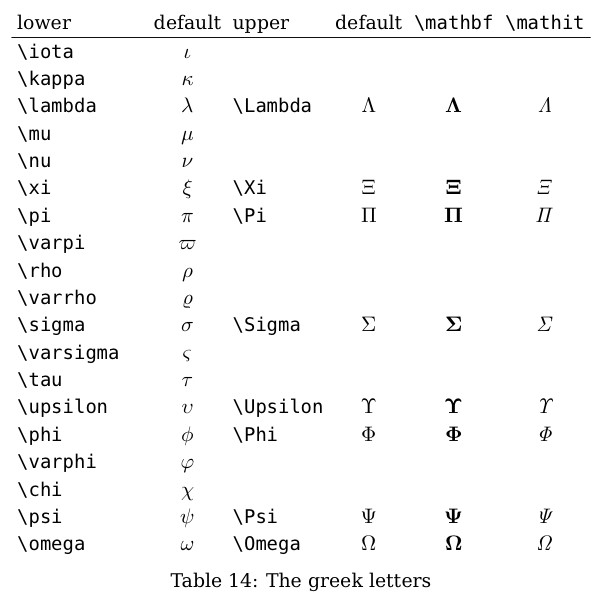
3、希腊字母

4、矩阵表示
$\left(
\begin{array}{ccc}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9 \\
\end{array}
\right)$
求和
\sum_{i=1}^{m}
我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。 即使得代价函数,$J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2$最小
极限
\lim_{n\to \infty}