在分类问题中,你要预测的变量 y 是离散的值,我们将学习一种叫做逻辑回归 (Logistic Regression) 的算法,这是目前最流行使用最广泛的一种学习算法。
在分类问题中,我们尝试预测的是结果是否属于某一个类(例如正确或错误)。分类问 题的例子有:判断一封电子邮件是否是垃圾邮件;判断一次金融交易是否是欺诈;之前我们 也谈到了肿瘤分类问题的例子,区别一个肿瘤是恶性的还是良性的。
我们可以用逻辑回归来解决分类问题
假说表示
我们引入一个新的模型,逻辑回归,该模型的输出变量范围始终在 0 和 1 之间。 逻辑 回归模型的假设是:$hθ(x)=g(θ^TX)$
X 代表特征向量
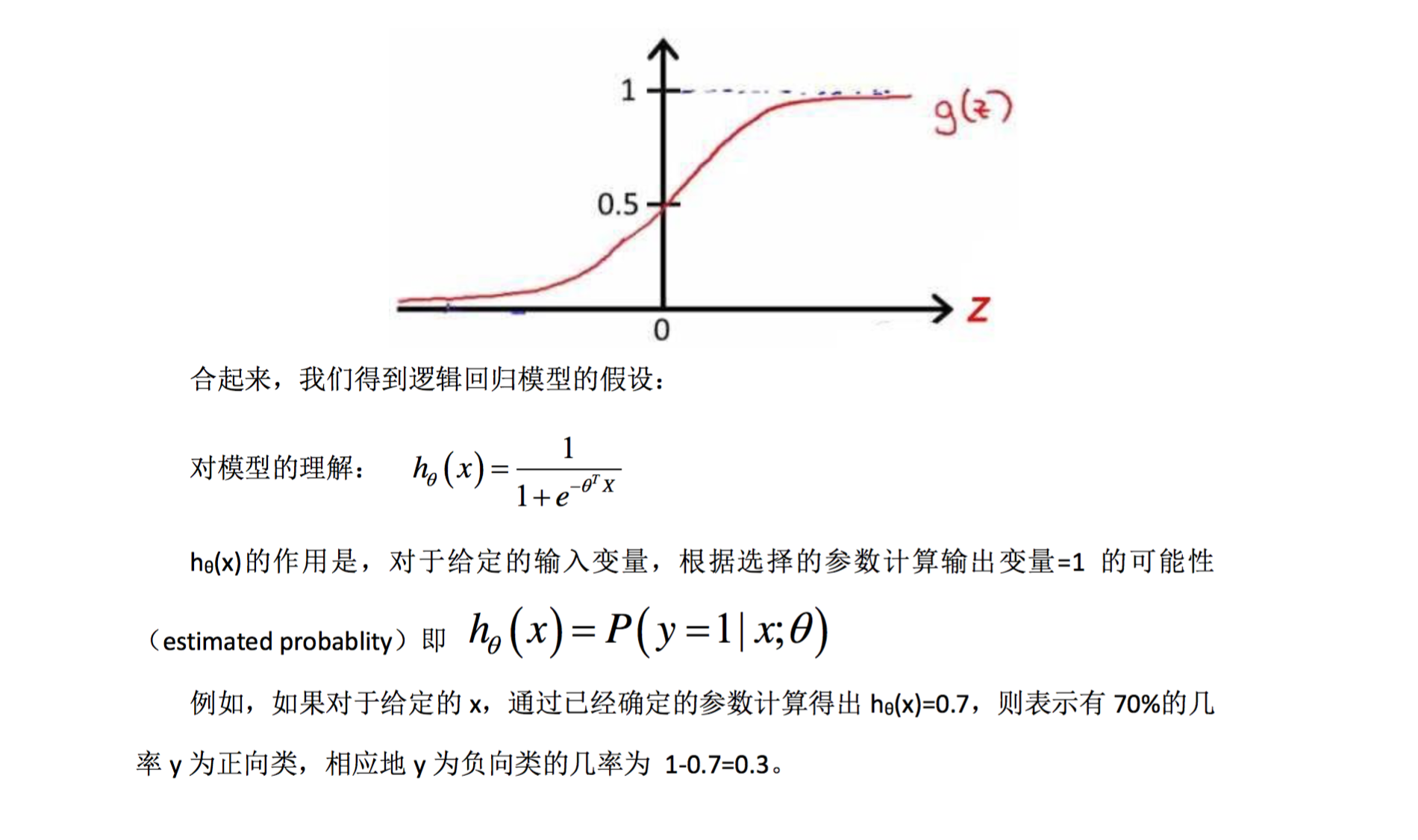
g 代表逻辑函数(logistic function)是一个常用的逻辑函数为 S 形函数(Sigmoid function),
公式为:$g(z)=\frac{1}{1+e^{-z}}$
该函数的图像为:
判定边界
在逻辑回归中,我们预测:
当 hθ 大于等于 0.5 时,预测 y=1
当 hθ 小于 0.5 时,预测 y=0 根据上面绘制出的 S 形函数图像,我们知道当 z=0 时 g(z)=0.5
z>0 时 g(z)>0.5
z<0 时 g(z)<0.5
又 $z=θ^TX$,即:
$θ^TX$ 大于等于 0 时,预测 y=1
$θ^TX$ 小于 0 时,预测 y=0
代价函数
在这段视频中,我们要介绍如何拟合逻辑回归模型的参数θ。具体来说,我要定义用来 拟合参数的优化目标或者叫代价函数,这便是监督学习问题中的逻辑回归模型的拟合问题。

对于线性回归模型,我们定义的代价函数是所有模型误差的平方和。理论上来说,我们 也可以对逻辑回归模型沿用这个定义,但是问题在于,当我们将逻辑回归
代入时, 这样定义了的代价函数中时,我们得到的代价函数将是一个非凸函数(non-convex function)
这意味着我们的代价函数有许多局部最小值,这将影响梯度下降算法寻找全局最小值。
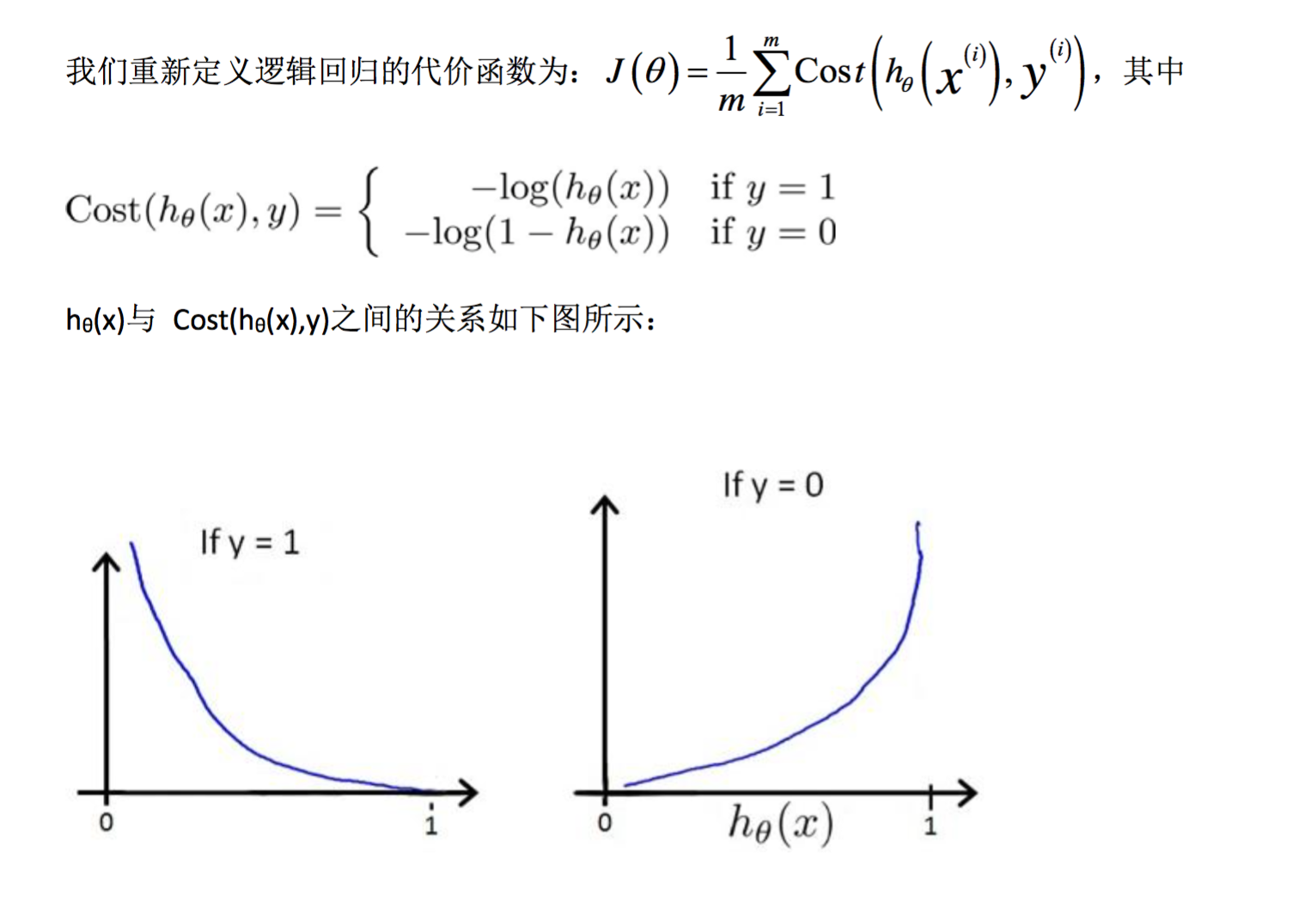
这样构建的 Cost(hθ(x),y)函数的特点是:当实际的 y=1 且 hθ 也为 1 时误差为 0,当 y=1 但 hθ 不为 1 时误差随着 hθ 的变小而变大;当实际的 y=0 且 hθ 也为 0 时代价为 0,当 y=0 但 hθ 不为 0 时误差随着 hθ 的变大而变大。
简化的成本函数和梯度下降
在这段视频中,我们将会找出一种稍微简单一点的方法来写代价函数,来替换我们现在 用的方法。同时我们还要弄清楚如何运用梯度下降法,来拟合出逻辑回归的参数。因此,听 了这节课,你就应该知道如何实现一个完整的逻辑回归算法。

最小化代价函数的方法,是使用梯度下降法(gradient descent)。这是我们的代价函数:

现在,如果你把这个更新规则和我们之前用在线性回归上的进行比较的话,你会惊讶地 发现,这个式子正是我们用来做线性回归梯度下降的。 那么,线性回归和逻辑回归是同一个算法吗?要回答这个问题,我们要观察逻辑回归看 看发生了哪些变化。实际上,假设的定义发生了变化。
对于线性回归假设函数: $h_\theta(x)=\Theta^TX$
而现在逻辑函数假设函数: $h_\theta(x)=\frac{1}{1+e^{-\theta^TX}}$
高级优化
现在我们换个角度来看什么是梯度下降,我们有个代价函数 J(θ),而我们想要使其最小 化,那么我们需要做的是编写代码,当输入参数 θ 时,它们会计算出两样东西:J(θ) 以及 J 等于 0、1 直到 n 时的偏导数项
假设我们已经完成了可以实现这两件事的代码,那么梯度下降所做的就是反复执行这些 更新。 另一种考虑梯度下降的思路是:我们需要写出代码来计算 J(θ) 和这些偏导数,然后把 这些插入到梯度下降中,然后它就可以为我们最小化这个函数。 对于梯度下降来说,我认为从技术上讲,你实际并不需要编写代码来计算代价函数 J(θ)。 你只需要编写代码来计算导数项,但是,如果你希望代码还要能够监控这些 J(θ) 的收敛性.那么我们就需要自己编写代码来计算代价函数 J(θ)和偏导数项
然而梯度下降并不是我们可以使用的唯一算法,还有其他一些算法,更高级、更复杂。
如果我们能用这些方法来计算代价函数 J(θ)和偏导数项两个项的话,那么这些算 j 法就是为我们优化代价函数的不同方法,
- 共轭梯度法
- BFGS (变尺度法)
- L-BFGS (限制变尺 度法)
就是其中一些更高级的优化算法,它们需要有一种方法来计算 J(θ),以及需要一种方 法计算导数项,然后使用比梯度下降更复杂的算法来最小化代价函数。这三种算法的具体细 节超出了本门课程的范畴。实际上你最后通常会花费很多天,或几周时间研究这些算法,你 可以专门学一门课来 高数值计算能力,不过让我来告诉你他们的一些特性:
这三种算法有许多优点: 一个是使用这其中任何一个算法,你通常不需要手动选择学习率 α,所以对于这些算法 的一种思路是,给出计算导数项和代价函数的方法,你可以认为算法有一个智能的内部循环, 而且,事实上,他们确实有一个智能的内部循环,称为线性搜索(line search)算法,它可以自 动尝试不同的学习速率 α,并自动选择一个好的学习速率 α,因此它甚至可以为每次迭代选 择不同的学习速率,那么你就不需要自己选择。这些算法实际上在做更复杂的事情,而不仅 仅是选择一个好的学习率,所以它们往往最终收敛得远远快于梯度下降,这些算法实际上在 做更复杂的事情,不仅仅是选择一个好的学习速率,所以它们往往最终比梯度下降收敛得快 多了,不过关于它们到底做什么的详细讨论,已经超过了本门课程的范围。
高级优化matlab实现

如果我们不知道最小值,但你想要代价函数找到这个最小值,是用比如梯度下降这些算 法,但最好是用比它更高级的算法,你要做的就是运行一个像这样的 matlab 函数:
function [jVal, gradient]=costFunction(theta)
jVal=(theta(1)-5)^2+(theta(2)-5)^2;
gradient=zeros(2,1);
gradient(1)=2*(theta(1)-5);
gradient(2)=2*(theta(2)-5);
end
这样就计算出这个代价函数,函数返回的第二个值是梯度值,梯度值应该是一个 2×1 的向量,梯度向量的两个元素对应这里的两个偏导数项,运行这个 costFunction 函数后,你 就可以调用高级的优化函数,这个函数叫 fminunc,它表示 Octave 里无约束最小化函数。 调用它的方式如下
options=optimset('GradObj','on','MaxIter',100);
initialTheta=zeros(2,1);
[optTheta, functionVal, exitFlag]=fminunc(@costFunction, initialTheta, options);
你要设置几个 options,这个 options 变量作为一个数据结构可以存储你想要的 options, 所以 GradObj 和 On,这里设置梯度目标参数为打开(on),这意味着你现在确实要给这个算 法 供一个梯度,然后设置最大迭代次数,比方说 100,我们给出一个 θ 的猜测初始值,它 是一个 2×1 的向量,那么这个命令就调用 fminunc,这个@符号表示指向我们刚刚定义的 costFunction 函数的指针。如果你调用它,它就会使用众多高级优化算法中的一个,当然你 也可以把它当成梯度下降,只不过它能自动选择学习速率 α,你不需要自己来做。然后它会 尝试使用这些高级的优化算法,就像加强版的梯度下降法,为你找到最佳的 θ 值。
多类别分类:一对多
在本节视频中,我们将谈到如何使用逻辑回归 (logistic regression)来解决多类别分类问 题,具体来说,我想通过一个叫做”一对多” (one-vs-all) 的分类算法。
先看这样一些例子。
假如说你现在需要一个学习算法能自动地将邮件归类到不同的文件夹里, 或者说可以自动地加上标签,那么,你也许需要一些不同的文件夹,或者不同的标签来完成 这件事,来区分开来自工作的邮件、来自朋友的邮件、来自家人的邮件或者是有关兴趣爱好 的邮件,那么,我们就有了这样一个分类问题:其类别有四个,分别用 y=1、y=2、y=3、y=4 来代表。
现在我们有一个训练集,好比上图表示的有三个类别,我们用三角形表示 y=1,方框表 示 y=2,叉叉表示 y=3。我们下面要做的就是使用一个训练集,将其分成三个二元分类问题。 我们先从用三角形代表的类别 1 开始,实际上我们可以创建一个,新的”伪”训练集,类 型 2 和类型 3 定为负类,类型 1 设定为正类,我们创建一个新的训练集,如下图所示的那
样,我们要拟合出一个合适的分类器。
接下来我们可以把类型二设定为正类,2,3为负类,再将3设定为正类,1,2为负类
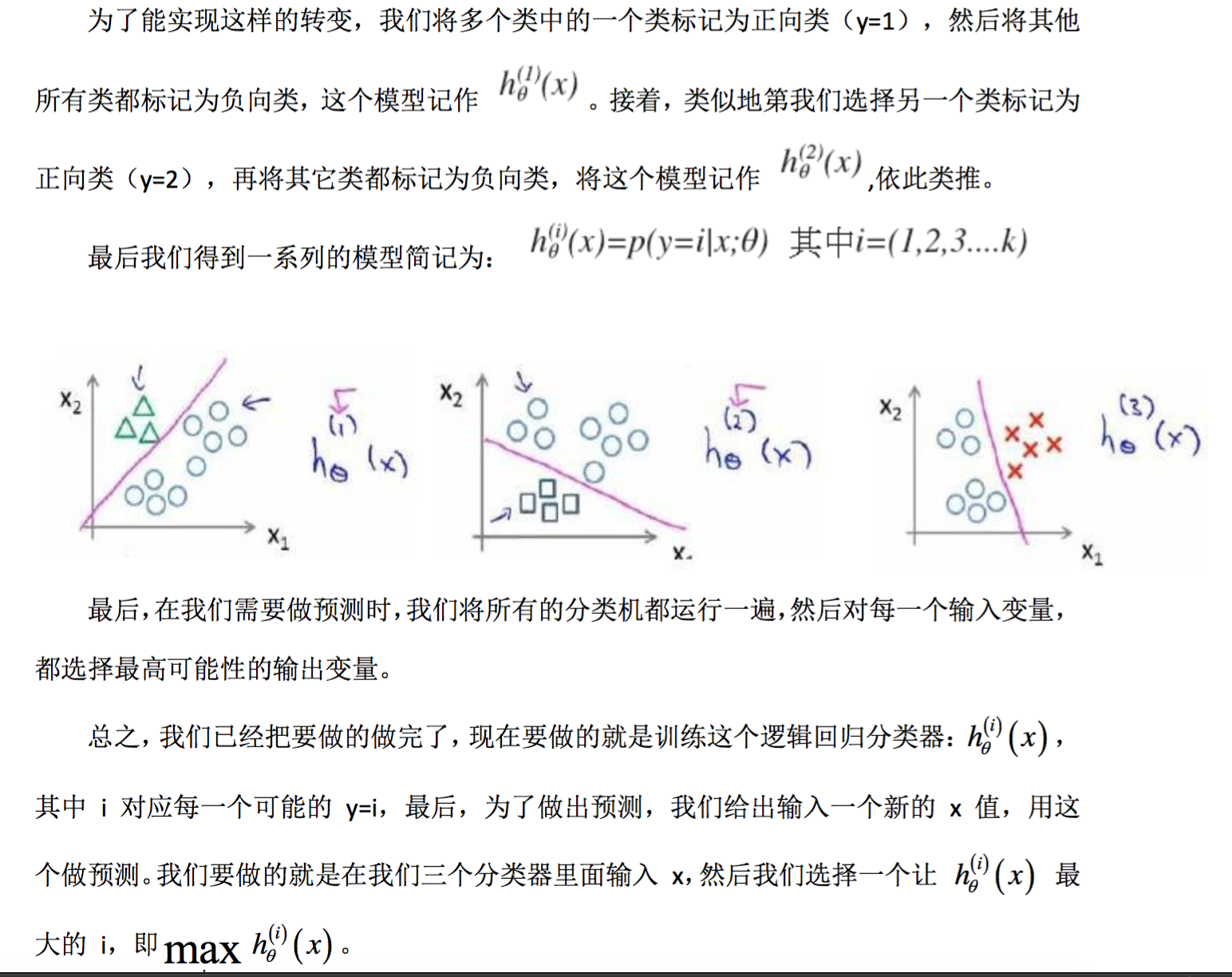
你现在知道了基本的挑选分类器的方法,选择出哪一个分类器是可信度最高效果最好的, 那么就可认为得到一个正确的分类,无论 i 值是多少,我们都有最高的概率值,我们预测 y 就是那个值。这就是多类别分类问题,以及一对多的方法,通过这个小方法,你现在也可以 将逻辑回归分类器用在多类分类的问题上。
正则化(Regularization)
过度拟合
如果我们有非常多的特征,我们通过学习得到的假设可能能够非常好地适应训练集(代 价函数可能几乎为 0),但是可能会不能推广到新的数据。
下图是一个回归问题的例子:
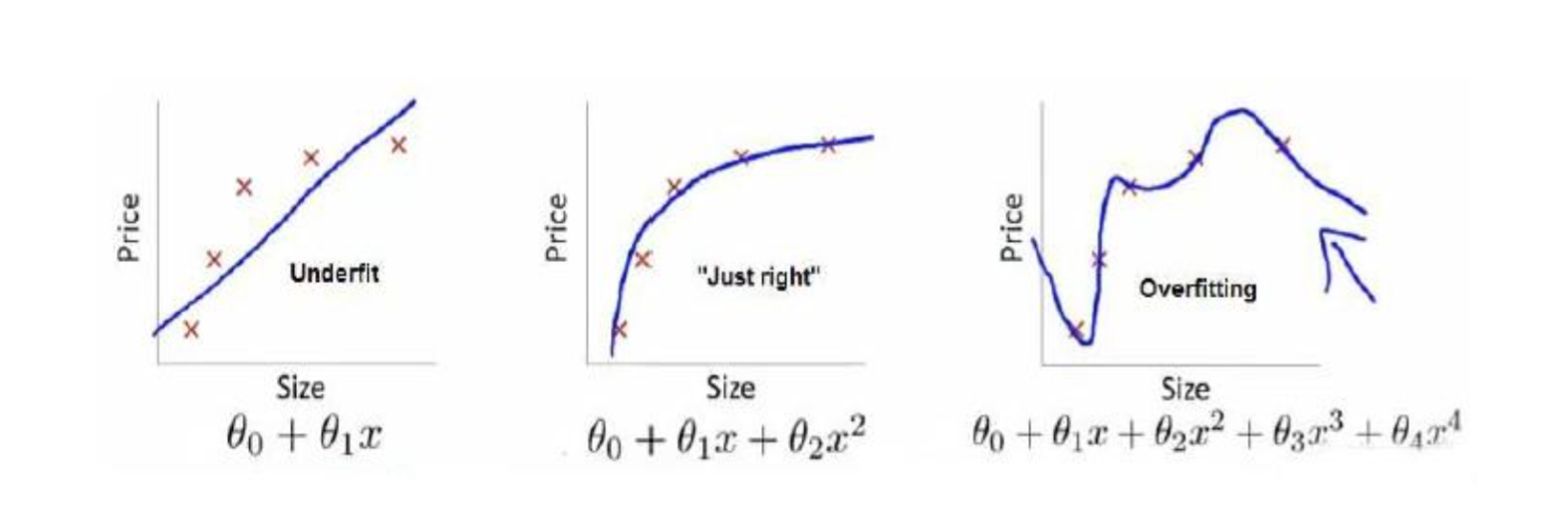
第一个模型是一个线性模型,欠拟合,不能很好地适应我们的训练集;第三个模型是一 个四次方的模型,过于强调拟合原始数据,而丢失了算法的本质:预测新数据。我们可以看 出,若给出一个新的值使之预测,它将表现的很差,是过拟合,虽然能非常好地适应我们的 训练集但在新输入变量进行预测时可能会效果不好;而中间的模型似乎最合适。
就以多项式理解,x 的次数越高,拟合的越好,但相应的预测的能力就可能变差。 问题是,如果我们发现了过拟合问题,应该如何处理?
- 丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征,或者使用 一些模型选择的算法来帮忙(例如 PCA)
- 正则化。 保留所有的特征,但是减少参数的大小(magnitude)。
代价函数
假如我们 有非常多的特征,我们并不知道其中哪些特征我们要惩罚,我们将对所有的特征进行惩罚, 并且让代价函数最优化的软件来选择这些惩罚的程度。这样的结果是得到了一个较为简单的 能防止过拟合问题的假设:
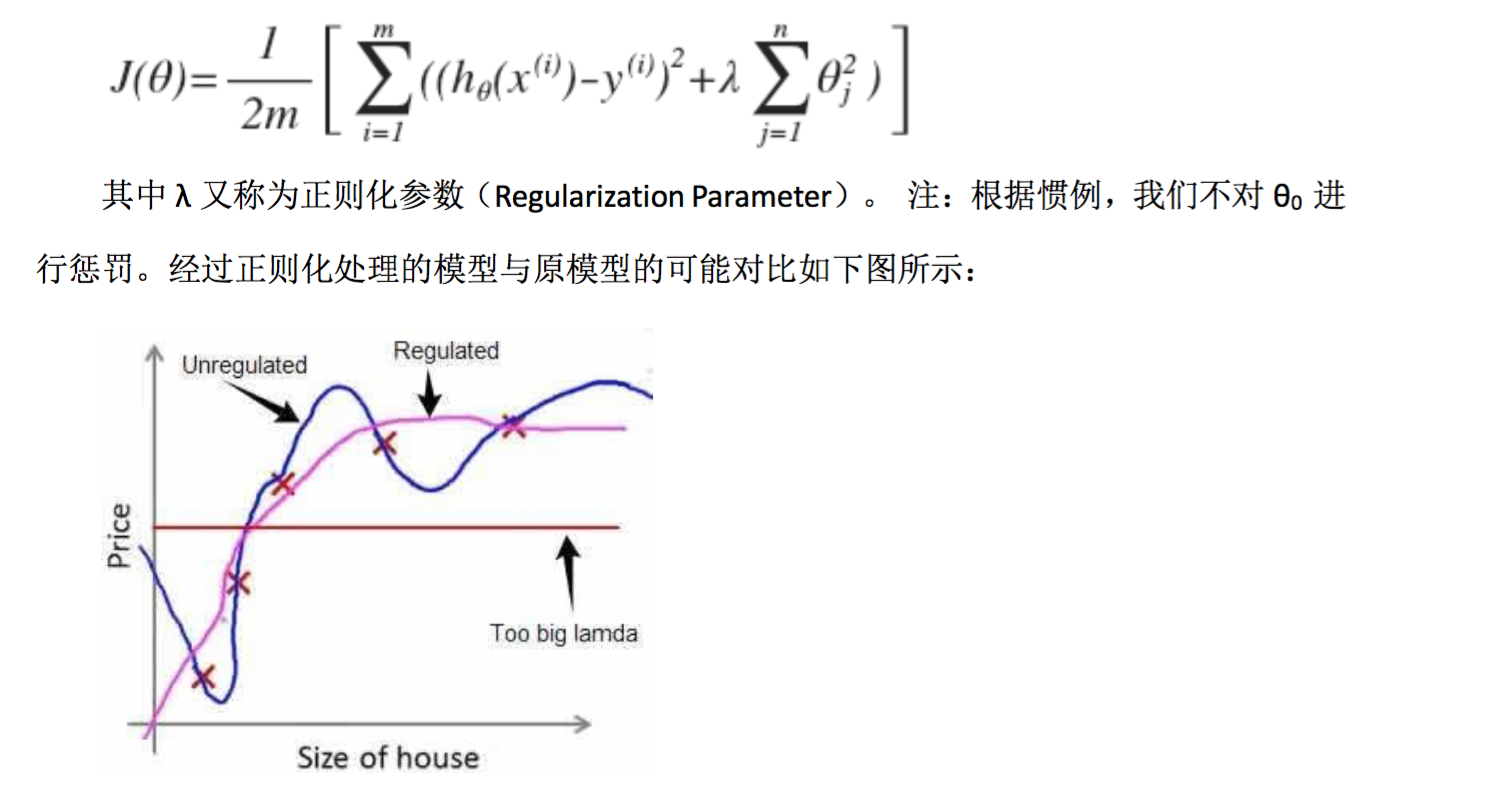
如果选择的正则化参数 λ 过大,则会把所有的参数都最小化了,导致模型变成 hθ(x)=θ0,也就是上图中红色直线所示的情况,造成欠拟合。
所以对于正则化,我们要取一个合理的λ的值,这样才能更好的应用正则化。
正则化线性回归
对于线性回归的求解,我们之前推导了两种学习算法:一种基于梯度下降,一种基于正 规方程。
正则化线性回归的代价函数为:

我们同样也可以利用正规方程来求解正则化线性回归模型,方法如下所示:
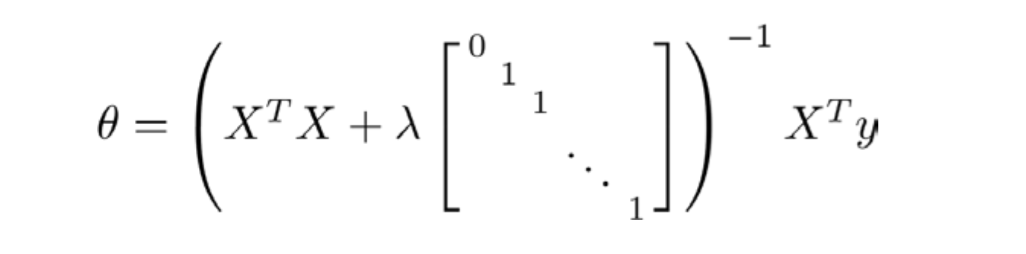
图中的矩阵尺寸为 (n+1)*(n+1)。
正则化的逻辑回归模型
针对逻辑回归问题,我们在之前的课程已经学习过两种优化算法:我们首先学习了使用 梯度下降法来优化代价函数 J(θ),接下来学习了更高级的优化算法,这些高级优化算法需要 你自己设计代价函数 J(θ)。

注意:
1.虽然正则化的逻辑回归中的梯度下降和正则化的线性回归中的表达式看起来一样,但 由于两者的 h(x)不同所以还是有很大差别。
- θ0 不参与其中的任何一个正则化。