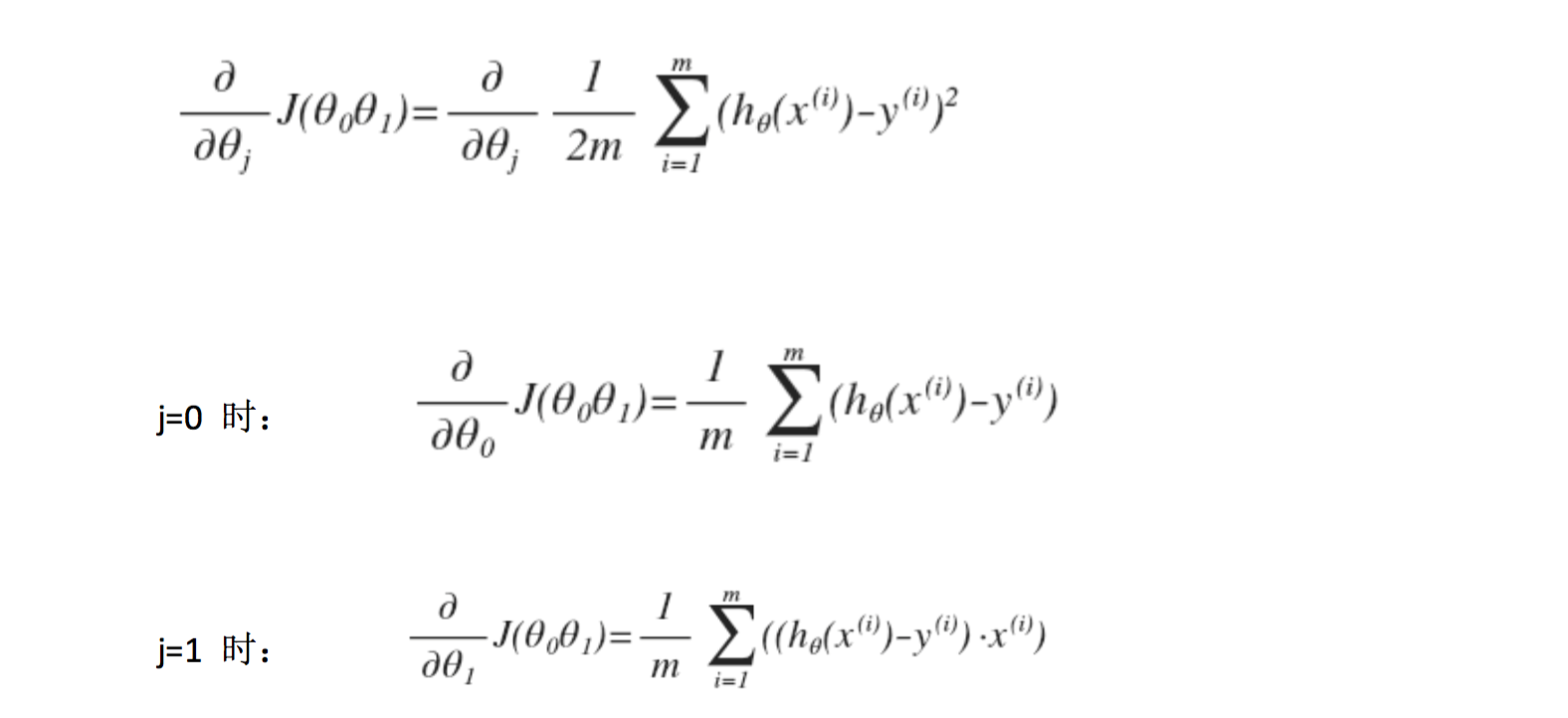很棒的一篇文章,梳理了机器学习的历史,发展,原理,与各项先进技术的关系等等:从机器学习谈起
机器学习是什么?
第一个机器学 习的定义来自于 Arthur Samuel。他定义机器学习为,在进行特定编程的情况下,给予计算机 学习能力的领域。 上述是个有点不正式的定义,也比较古老。另一个年代近一点 的定义,由 Tom Mitchell 提出,来自卡内基梅隆大学,Tom 定义的机器学习是,一个好的学 习问题定义如下,他说,一个程序被认为能从经验 E 中学习,解决任务 T,达到性能度量值 P,当且仅当,有了经验 E 后,经过 P 评判,程序在处理 T 时的性能有所提升。我认为经验 e 就是程序上万次的自我练习的经验而任务 t 就是下棋。性能度量值 p 呢,就是它在与一 些新的对手比赛时,赢得比赛的概率。
机器学习算法
- 监督学习
- 非监督学习
最常见的两种
监督学习
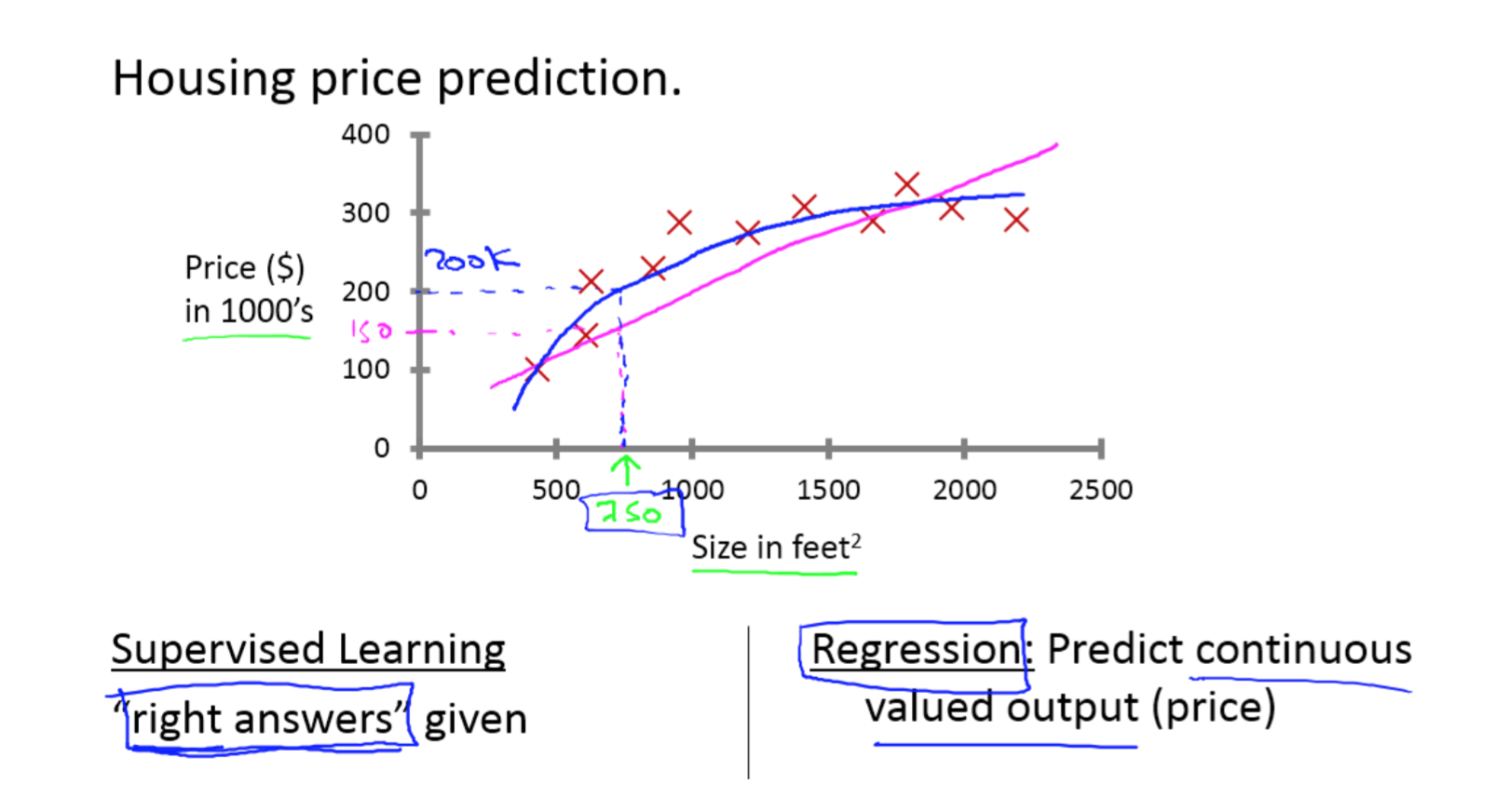
监督学习指的就是我们给学习算法一个数据集。这个数据集由“正确答案” 组成。在房价的例子中,我们给了一系列房子的数据,我们给定数据集中每个样本的正确价 格,即它们实际的售价然后运用学习算法,算出更多的正确答案。比如你朋友那个新房子的 价格。用术语来讲,这叫做回归问题。
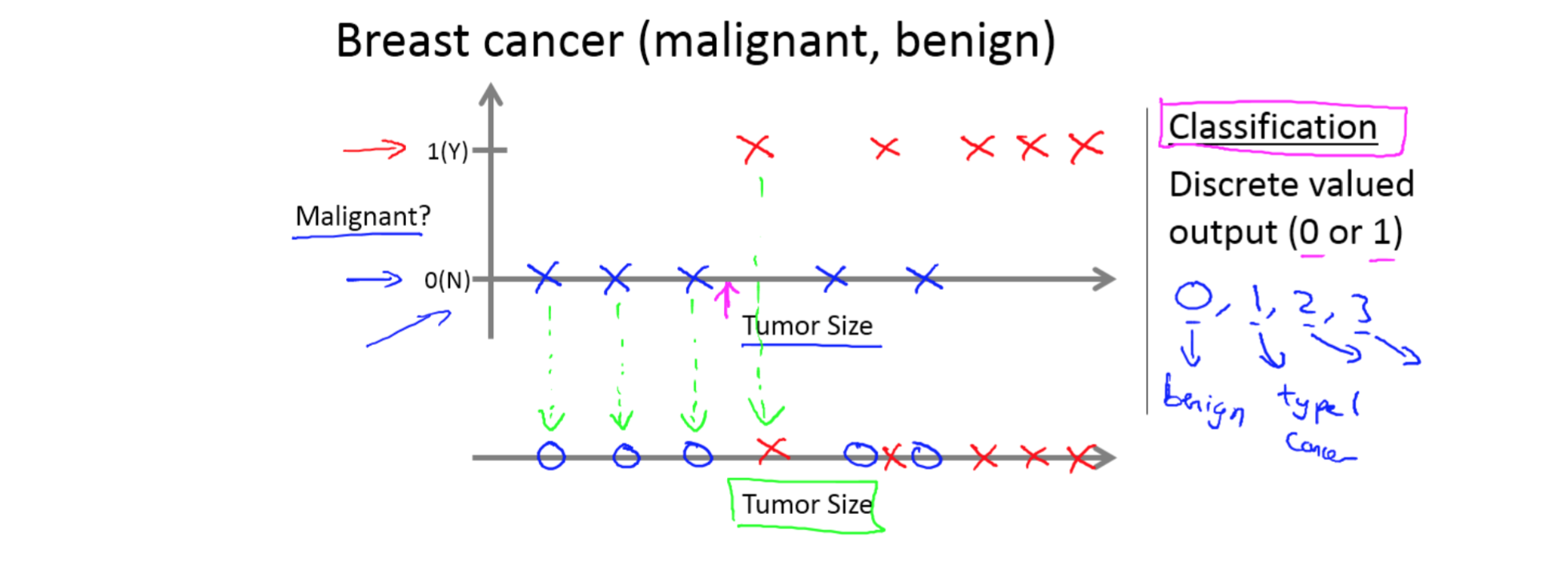
让我们来看一组数据:这个数据集中,横轴表示肿瘤的大小,纵轴上,我标出 1 和 0 表 示是或者不是恶性肿瘤。我们之前见过的肿瘤,如果是恶性则记为 1 ,不是恶性,或者说良 性记为 0。 我有 5 个良性肿瘤样本,在 1 的位置有 5 个恶性肿瘤样本。现在我们有一个朋友很不幸 检查出乳腺肿瘤。假设说她的肿瘤大概这么大,那么机器学习的问题就在于,你能否估算出 肿瘤是恶性的或是良性的概率。用术语来讲,这是一个分类问题。
现在来回顾一下,这节课我们介绍了监督学习。其基本思想是,我们数据集中的每个样 本都有相应的“正确答案”。再根据这些样本作出预测,就像房子和肿瘤的例子中做的那样。 我们还介绍了回归问题,即通过回归来推出一个连续的输出,之后我们介绍了分类问题,其 目标是推出一组离散的结果。
无监督学习
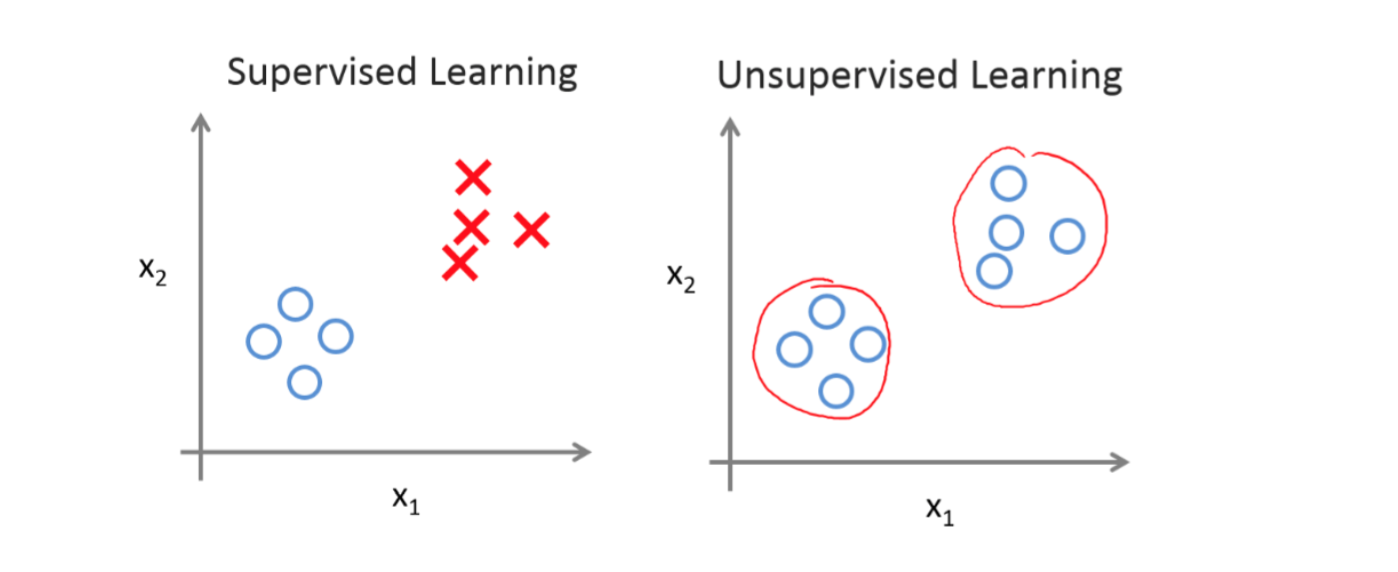
在无监督学习中,我们已知的数据。看上去有点不一样,不同于监督学习的数据的样子, 即无监督学习中没有任何的标签或者是有相同的标签或者就是没标签。所以我们已知数据 集,却不知如何处理,也未告知每个数据点是什么。别的都不知道,就是一个数据集。你能 从数据中找到某种结构吗?针对数据集,无监督学习就能判断出数据有两个不同的聚集簇。 这是一个,那是另一个,二者不同。是的,无监督学习算法可能会把这些数据分成两个不同 的簇。所以叫做聚类算法。事实证明,它能被用在很多地方。
单变量线性回归(Linear Regression with One Variable)
我们将引入一些符号来表示我们的回归方程
- m代表训练集中实例的数量 - x代表特征/输入变量 - y代表目标变量/输出变量 - (x,y) 代表训练集中的实例 - (x(i),y(i) ) 代表第 i 个观察实例
- h代表学习算法的解决方案或函数也称为假设(hypothesis)
代价函数
在线性回归中我们有一个像这样的训练集,m 代表了训练样本的数量,比如 m = 47。 而我们的假设函数,也就是用来进行预测的函数,是这样的线性函数形式:$h_0(x)=\theta_0+\theta_1*x$
接下来我们会引入一些术语我们现在要做的便是为我们的模型选择合适的参数 (parameters)$θ_0$ 和 $θ_1$,在房价问题这个例子中便是直线的斜率和在 y 轴上的截距。 我们选择的参数决定了我们得到的直线相对于我们的训练集的准确程度,模型所预测的 值与训练集中实际值之间的差距(下图中蓝线所指)就是建模误差(modeling error)。
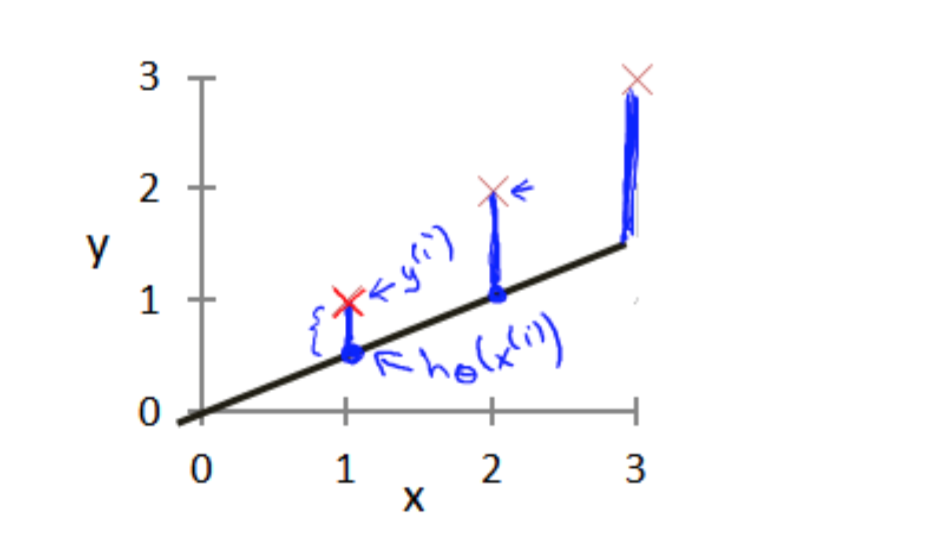
我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。 即使得代价函数,$J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2$最小
代价函数的直观理解
在上一个视频中,我们给了代价函数一个数学上的定义。在这个视频里,让我们通过一 些例子来获取一些直观的感受,看看代价函数到底是在干什么。

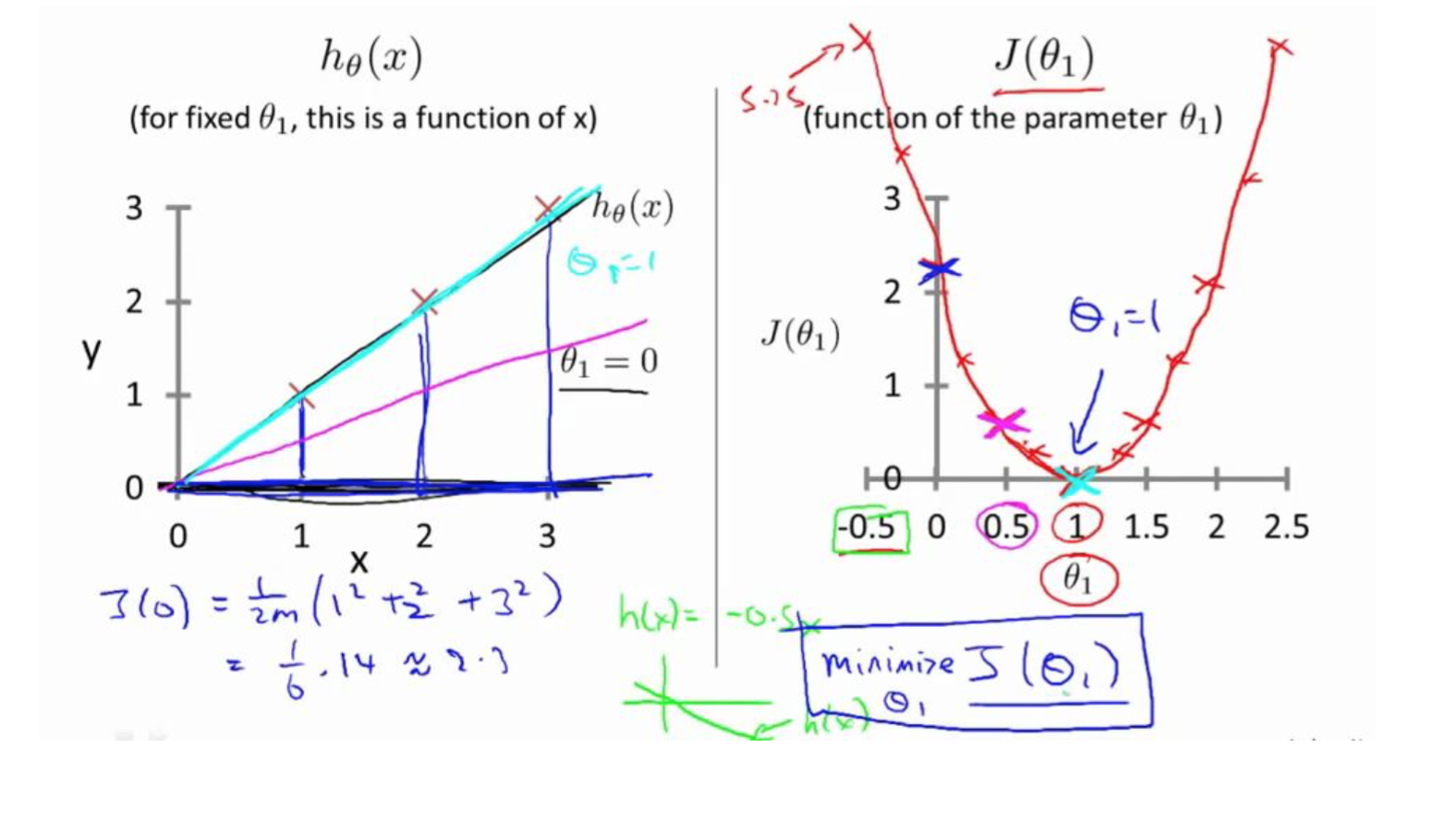
梯度下降算法
梯度下降是一个用来求函数最小值的算法,我们将使用梯度下降算法来求出代价函数的最小值
梯度下降背后的思想是:开始时我们随机选择一个参数的组合$(θ_0,θ_1,…,θ_n)$,计算代价 函数,然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到到 一个局部最小值(local minimum),因为我们并没有尝试完所有的参数组合,所以不能确定 我们得到的局部最小值是否便是全局最小值(global minimum),选择不同的初始参数组合, 可能会找到不同的局部最小值。

其中 α 是学习率(learning rate),它决定了我们沿着能让代价函数下降程度最大的方 向向下迈出的步子有多大,在批量梯度下降中,我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数
在梯度下降算法中,还有一个更微妙的问题,梯度下降中,我们要更新 θ0 和 θ1 ,当 j=0 和 j=1 时,会产生更新,所以你将更新 Jθ0 和 Jθ1。实现梯度下降算法的微妙之处是,在这 个表达式中,如果你要更新这个等式,你需要同时更新 θ0 和 θ1
梯度下降的直观理解
如果 α 太小了,即我的学习速率太小,结果就是只能这样像小宝宝一样一点点地挪动, 去努力接近最低点,这样就需要很多步才能到达最低点,所以如果 α 太小的话,可能会很慢 因为它会一点点挪动,它会需要很多步才能到达全局最低点。 如果 α 太大,那么梯度下降法可能会越过最低点,甚至可能无法收敛,下一次迭代又移 动了一大步,越过一次,又越过一次,一次次越过最低点,直到你发现实际上离最低点越来越远,所以,如果 α 太大,它会导致无法收敛,甚至发散。
梯度下降的线性回归
在以前的视频中我们谈到关于梯度下降算法,梯度下降是很常用的算法,它不仅被用在 线性回归上和线性回归模型、平方误差代价函数。在这段视频中,我们要将梯度下降和代价 函数结合。我们将用到此算法,并将其应用于具体的拟合直线的线性回归算法里。
对我们之前的线性回归问题运用梯度下降法,关键在于求出代价函数的导数,即: